��Ŀ����
2�����壺��A��B�Ƿǿյ�������a��A��b��B����a��b�ĺ�����bҲ��a�ĺ��������a��b�ǡ���г��ϵ�������ʽb=a2��a��[0��+�ޣ���a��b�ǡ���г��ϵ���������е���a��b�ǡ���г��ϵ�����ǣ�������| A�� | $b=\frac{sina}{a}��a�ʣ�0��\frac{��}{2}��$ | B�� | $b={a^3}+\frac{5}{2}{a^2}+2a+1��a�ʣ�-2��-\frac{2}{3}��$ | ||
| C�� | ��a-2��2+b2=1��a��[1��2] | D�� | |a|+|b|=1��a��[-1��1] |
���� ֻҪ�ж��������ĺ����������ɣ�
��� �⣺A����$a�ʣ�0��\frac{��}{2}��$����a��sina����b��=$\frac{acosa-sina}{{a}^{2}}$=$\frac{cosa��a-sina��}{{a}^{2}}$��0����˺���b��$a�ʣ�0��\frac{��}{2}��$�ϵ�����������ȷ��
B����a��$��-2��-\frac{2}{3}��$��b��=3a2+5a+2=��3a+2����a+1������a�ʣ�-2��-1��ʱ����������a�ʣ�-1��-$\frac{2}{3}$��ʱ�����ݼ�����˲��������⣻
C���ߣ�a-2��2+b2=1��a��[1��2]����b=��$\sqrt{1-��a-2��^{2}}$��b����a�ĺ�������ȥ��
D����|a|+|b|=1��a��[-1��1]����b=����1-|a|����b����a�ĺ�������ȥ��
��ѡ��A��
���� ���⿼�������õ����о������ĵ����ԡ��¶��塰��г��������������������������������������е��⣮

��ϰ��ϵ�д�
 �����ÿ�ʱѵ��ϵ�д�
�����ÿ�ʱѵ��ϵ�д� ��Ԫȫ��������ϵ�д�
��Ԫȫ��������ϵ�д� �»ƸԱ����ܾ�ϵ�д�
�»ƸԱ����ܾ�ϵ�д�
�����Ŀ
10��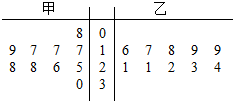 ijУΪ�˽����ѧ��Ӣ���������������˼ס��������ʮ��ѧ����һ��Ӣ�������ɼ����������������þ�Ҷͼ��ʾ����ͼ��ʾ�����������ж���ȷ���ǣ�������
ijУΪ�˽����ѧ��Ӣ���������������˼ס��������ʮ��ѧ����һ��Ӣ�������ɼ����������������þ�Ҷͼ��ʾ����ͼ��ʾ�����������ж���ȷ���ǣ�������
 ijУΪ�˽����ѧ��Ӣ���������������˼ס��������ʮ��ѧ����һ��Ӣ�������ɼ����������������þ�Ҷͼ��ʾ����ͼ��ʾ�����������ж���ȷ���ǣ�������
ijУΪ�˽����ѧ��Ӣ���������������˼ס��������ʮ��ѧ����һ��Ӣ�������ɼ����������������þ�Ҷͼ��ʾ����ͼ��ʾ�����������ж���ȷ���ǣ�������| A�� | �������ݵ�����Ϊ28 | B�� | �������ݵ���λ����22 | ||
| C�� | �������ݵ����ֵΪ30 | D�� | �������ݵļ���Ϊ16 |
17��ij��˾Ϊȷ����һ���Ͷ��ij�ֲ�Ʒ�������ѣ����˽���������x����λ����Ԫ������������y����λ���֣���Ӱ�죬Ϊ�˶Խ�6�����������x����λ����Ԫ������������y����λ���֣������ݽ���������������ͳ�Ʊ���
�����ɱ�������������Իع鷽��$\hat y=\hat bx+\hat a$�е�$\hat b��0.6$�������$\hat a$��ֵ��
������֪���ֲ�Ʒ��������z����λ����Ԫ����x��y֮��Ĺ�ϵΪz=30y-x2�����ݣ���������Ļع鷽�̣�����������xΪ��ֵʱ��������z��Ԥ��ֵ���
| x����Ԫ�� | 2 | 3 | 4.5 | 5 | 7.5 | 8 |
| y���֣� | 3 | 3.5 | 3.5 | 4 | 6 | 7 |
������֪���ֲ�Ʒ��������z����λ����Ԫ����x��y֮��Ĺ�ϵΪz=30y-x2�����ݣ���������Ļع鷽�̣�����������xΪ��ֵʱ��������z��Ԥ��ֵ���
7��PM2.5��ָ������ֱ��С�ڻ����2.5�Ŀ����Ҳ�ƿ���ο������Ϊ��̽����������PM2.5��Ũ���Ƿ���أ��ֲɼ���ij������һ������ijһʱ��γ�������PM2.5���������±���
�������ϱ��������y��x�����Իع�ֱ�߷���$\hat y=\hat bx+\hat a$��
����������ͬһʱ��γ�������25�������Ը��ݣ�������������Իع鷽��Ԥ���ʱPM2.5��Ũ���Ƕ��٣�������������
�ο���ʽ����$\stackrel{��}{b}$=$\frac{\sum_{i=1}^{n}��{x}_{i}-\overline{x}����{y}_{i}-\overline{y}��}{\sum_{i=1}^{n}��{x}_{i}-\overline{x}��^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$������$\hat y=\hat bx+\hat a$��
| ʱ�� | ��һ | �ܶ� | ���� | ���� | ���� |
| ������x�������� | 50 | 51 | 54 | 57 | 58 |
| PM2.5��Ũ��y����/�����ף� | 69 | 70 | 74 | 78 | 79 |
����������ͬһʱ��γ�������25�������Ը��ݣ�������������Իع鷽��Ԥ���ʱPM2.5��Ũ���Ƕ��٣�������������
�ο���ʽ����$\stackrel{��}{b}$=$\frac{\sum_{i=1}^{n}��{x}_{i}-\overline{x}����{y}_{i}-\overline{y}��}{\sum_{i=1}^{n}��{x}_{i}-\overline{x}��^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$������$\hat y=\hat bx+\hat a$��
14������˵��������ǣ�������
| A�� | ���⡰��x2-3x+2=0����x=1�����������Ϊ����x��1����x2-3x+2��0�� | |
| B�� | ������p����?x��R��x2-x-1��0����������p�ķ�Ϊ��?x��R��x2-x-1��0�� | |
| C�� | ��x=1���ǡ�x2+5x-6=0���ij�ֲ���Ҫ���� | |
| D�� | ��a=1���ǡ�ֱ��x-ay=0��ֱ��x+ay=0��Ϊ��ֱ���ij�Ҫ���� |
11����z��1+i��=i����|z|=��������
| A�� | $\frac{1}{2}$ | B�� | $\frac{\sqrt{2}}{2}$ | C�� | $\frac{\sqrt{3}}{2}$ | D�� | 2 |