题目内容
13.点P(0,4)关于x-y+3=0的对称点Q在直线l上,且l与直线3x-y+2=0平行(1)求直线l的方程
(2)求圆心在直线l上,与x轴相切,且被直线x-2y=0截得的弦长为4的圆的方程.
分析 (1)求出点(0,4)关于x-y+3=0的对称点,利用l与直线3x-y+2=0平行,即可求直线l的方程
(2)利用待定系数法,即可求出圆的方程.
解答 解:(1)设点Q(m,n)为点(0,4)关于x-y+3=0的对称点.
则$\left\{\begin{array}{l}{\frac{n-4}{m}=-1}\\{\frac{m}{2}-\frac{n+4}{2}+3=0}\end{array}\right.$(2分)
解得m=1,n=3,即Q(1,3).(3分)
由l与直线3x-y+2=0平行,得l的斜率为3.(4分)
又Q(1,3)在直线l上,
所以直线l的方程为y-3=3(x-1),即3x-y=0.(5分)
(2)设圆的方程为(x-a)2+(y-b)2=r2(r>0).
由题意得$\left\{\begin{array}{l}{3a-b=0}\\{|b|=r}\\{(\frac{|a-2b|}{\sqrt{5}})^{2}+{2}^{2}={r}^{2}}\end{array}\right.$(7分)
解得$\left\{\begin{array}{l}{a=-1}\\{b=-3}\\{r=3}\end{array}\right.$或$\left\{\begin{array}{l}{a=1}\\{b=3}\\{r=3}\end{array}\right.$.(9分)
∴圆的方程为(x+1)2+(y+3)2=9或(x-1)2+(y-3)2=9.(10分)
点评 本题主要考查求圆的标准方程的方法,求出圆心坐标和半径的值,是解题的关键,属于中档题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
2.定义:设A,B是非空的数集,a∈A,b∈B,若a是b的函数且b也是a的函数,则称a与b是“和谐关系”.如等式b=a2,a∈[0,+∞)中a与b是“和谐关系”,则下列等中a与b是“和谐关系”的是( )
| A. | $b=\frac{sina}{a},a∈(0,\frac{π}{2})$ | B. | $b={a^3}+\frac{5}{2}{a^2}+2a+1,a∈(-2,-\frac{2}{3})$ | ||
| C. | (a-2)2+b2=1,a∈[1,2] | D. | |a|+|b|=1,a∈[-1,1] |
3.某地区2007年至2013年农村居民家庭人均纯收入y(单位:千元)的数据如表:
(Ⅰ)求y关于t的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2017年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{t}$.
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(Ⅱ)利用(Ⅰ)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2017年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{t}$.
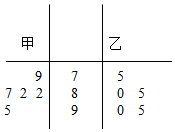 甲、乙两位学生参加某项竞赛培训,在培训期间,他们参加的5项预赛成绩的茎叶图记录如下:
甲、乙两位学生参加某项竞赛培训,在培训期间,他们参加的5项预赛成绩的茎叶图记录如下: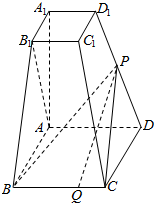 已知四棱台ABCD-A1B1C1D1的上下底面分别是边长为2和4的正方形,AA1=4且AA1⊥底面ABCD,点P为DD1的中点,Q为BC边上的一点.
已知四棱台ABCD-A1B1C1D1的上下底面分别是边长为2和4的正方形,AA1=4且AA1⊥底面ABCD,点P为DD1的中点,Q为BC边上的一点.