题目内容
12．若$a={（{\frac{3}{5}}）^4}，b={（{\frac{3}{5}}）^3}，c={log_3}\frac{3}{5}$，则a，b，c三者的大小关系为c＜a＜b．（用＜表示）．分析 根据对数函数和指数函数比较a，b，c与0，1的关系，即可得到答案．
解答 解：∵$a={（{\frac{3}{5}}）^4}，b={（{\frac{3}{5}}）^3}，c={log_3}\frac{3}{5}$，
∴0＜a＜b＜1，c＜0，
∴c＜a＜b，
故答案为：c＜a＜b．
点评 本题主要考查了指数函数和对数函数的图象和性质，关键是找到和0，1和关系，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
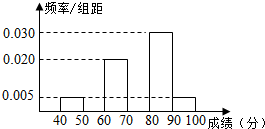某学校团委组织了“文明出行，爱我中华”的知识竞赛，从参加考试的学生中抽出60名学生，将其成绩（单位：分）整理后，得到如下频率分布直方图（其中分组区间为[40，50），[50，60），…，[90，100]），已知成绩在[50，60 ）的学生有9人，
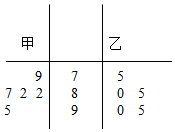甲、乙两位学生参加某项竞赛培训，在培训期间，他们参加的5项预赛成绩的茎叶图记录如下：
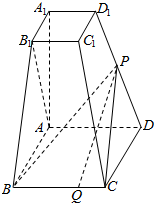已知四棱台ABCD-A1B1C1D1的上下底面分别是边长为2和4的正方形，AA1=4且AA1⊥底面ABCD，点P为DD1的中点，Q为BC边上的一点．
2．定义：设A，B是非空的数集，a∈A，b∈B，若a是b的函数且b也是a的函数，则称a与b是“和谐关系”．如等式b=a2，a∈[0，+∞）中a与b是“和谐关系”，则下列等中a与b是“和谐关系”的是（ ）
| A． | $b=\frac{sina}{a}，a∈（0，\frac{π}{2}）$ | B． | $b={a^3}+\frac{5}{2}{a^2}+2a+1，a∈（-2，-\frac{2}{3}）$ | ||
| C． | （a-2）2+b2=1，a∈[1，2] | D． | |a|+|b|=1，a∈[-1，1] |