题目内容
7.PM2.5是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物).为了探究车流量与PM2.5的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与PM2.5得数据如下表:| 时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
| 车流量x(万辆) | 50 | 51 | 54 | 57 | 58 |
| PM2.5的浓度y(微克/立方米) | 69 | 70 | 74 | 78 | 79 |
(Ⅱ)若周六同一时间段车流量是25万辆,试根据(Ⅰ)中求出的线性回归方程预测此时PM2.5的浓度是多少?(保留整数)
参考公式其中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$:方程$\hat y=\hat bx+\hat a$.
分析 (Ⅰ)根据表中数据,计算$\overline{x}$、$\overline{y}$与$\sum_{i=1}^{5}$(xi-$\overline{x}$)(yi-$\overline{y}$)和$\sum_{i=1}^{5}$${{(x}_{i}-\overline{x})}^{2}$的值,求出$\stackrel{∧}{b}$与$\stackrel{∧}{a}$,写出线性回归方程;
(Ⅱ)计算x=25时$\stackrel{∧}{y}$的值,即可预测出PM2.5的浓度.
解答 解:(Ⅰ)根据表中数据,得;
$\overline{x}$=$\frac{1}{5}$(50+51+54+57+58)=54,
$\overline{y}$=$\frac{1}{5}$(69+70+74+78+79)=74,…(2分)
$\sum_{i=1}^{5}$(xi-$\overline{x}$)(yi-$\overline{y}$)=4×5+3×4+3×4+4×5=64,
$\sum_{i=1}^{5}$${{(x}_{i}-\overline{x})}^{2}$=(-4)2+(-3)2+32+42=50,
∴$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{64}{50}$=1.28,…(4分)
$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$=74-1.28×54=4.88,…(6分)
故y关于x的线性回归方程是:$\stackrel{∧}{y}$=1.28x+4.88;…(8分)
(Ⅱ)当x=25时,$\stackrel{∧}{y}$=1.28×25+4.88=36.88≈37,
所以可以预测此时PM2.5的浓度约为37.…(12分)
点评 本题考查了线性回归方程的求法与应用问题,也考查了计算能力的应用问题,是基础题目.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $b=\frac{sina}{a},a∈(0,\frac{π}{2})$ | B. | $b={a^3}+\frac{5}{2}{a^2}+2a+1,a∈(-2,-\frac{2}{3})$ | ||
| C. | (a-2)2+b2=1,a∈[1,2] | D. | |a|+|b|=1,a∈[-1,1] |
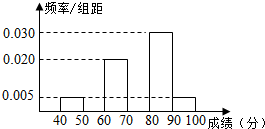 某学校团委组织了“文明出行,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(单位:分)整理后,得到如下频率分布直方图(其中分组区间为[40,50),[50,60),…,[90,100]),已知成绩在[50,60 )的学生有9人,
某学校团委组织了“文明出行,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(单位:分)整理后,得到如下频率分布直方图(其中分组区间为[40,50),[50,60),…,[90,100]),已知成绩在[50,60 )的学生有9人,