题目内容
某社区四支篮球队参加比赛，现任意将这四支队分成两个组（每组两个队）进行比赛，胜者再赛，则所有可能的比赛情况共有（ ）
| A、3种 | B、6种 |
| C、12种 | D、24种 |
考点：排列、组合的实际应用
专题：计算题,排列组合
分析：甲可能和另外的3个队中的一队一组，所以分组情况有3种，然后每对中胜者有2种情况，最后的胜者有2种情况，由乘法原理可得结论．
解答：
解：甲可能和另外的3个队中的一队一组，所以分组情况有3种．
这里不考虑两组有差别，即甲乙-丙丁，和丙丁-甲乙，属同一种情况，
然后每对中胜者有2种情况，最后的胜者有2种情况，
所以共有3×2×2=12种．
故选：C．
这里不考虑两组有差别，即甲乙-丙丁，和丙丁-甲乙，属同一种情况，
然后每对中胜者有2种情况，最后的胜者有2种情况，
所以共有3×2×2=12种．
故选：C．
点评：本题考查乘法原理的运用，考查学生分析解决问题的能力，属于基础题．
练习册系列答案
相关题目
设函数f（x）=x2-ax+b，a，b∈R．
（1）已知f（x）在区间（-∞，1）上单调递减，求a的取值范围；
（2）存在实数a，使得当x∈[0，b]时，2≤f（x）≤6恒成立，求b的最大值及此时a的值．
（1）已知f（x）在区间（-∞，1）上单调递减，求a的取值范围；
（2）存在实数a，使得当x∈[0，b]时，2≤f（x）≤6恒成立，求b的最大值及此时a的值．
某三棱锥的三视图如图所示，则这个三棱锥的体积为(
-
)8二项展开式中的常数项为（ ）
| 3 | x |
| 2 |
| x |
| A、56 | B、112 |
| C、-56 | D、-112 |
已知圆C的圆心是直线x-y+1=0与x轴的交点，且圆C与直线x+y+3=0相切，则圆C的方程是（ ）
| A、（x+1）2+y2=2 |
| B、（x+1）2+y2=8 |
| C、（x-1）2+y2=2 |
| D、（x-1）2+y2=8 |
（理）已知函数f（x）是定义在实数集R上的以2为周期的偶函数，当0≤x≤1时，f（x）=x2．若直线y=x+a与函数y=f（x）的图象在[0，2]内恰有两个不同的公共点，则实数a的值是（ ）
A、-
| ||||
| B、0 | ||||
C、0或-
| ||||
D、0或-
|
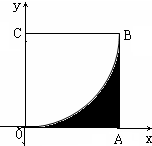如图，已知正方形OABC的四个顶点坐标分别为O（0，0），A（1，0），B（1，1），C（0，1），现向该正方体内部随机投1000个点，统计出所投点落在阴影部分的个数为328，由此估计图中阴影部分的面积为（ ）| A、0.328 | B、0.672 |
| C、0.3 | D、0.7 |
已知四棱锥P-ABCD的三视图如图所示，则四棱锥的外接球的表面积为（ ）| A、24π | ||
| B、6π | ||
C、
| ||
| D、3π |
如图所示，在直三棱柱ABC-A1B1C1中，AB=BB1，AC1⊥平面A1BD，D为AC的中点．