Question

【题目】如图，已知抛物线：，过焦点斜率大于零的直线交抛物线于、两点，且与其准线交于点．

（Ⅰ）若线段的长为，求直线的方程；

（Ⅱ）在上是否存在点，使得对任意直线，直线，，的斜率始终成等差数列，若存在求点的坐标；若不存在，请说明理由.

Answer 1

【答案】（Ⅰ）；（Ⅱ）存在点或，使得对任意直线，直线，，的斜率始终成等差数列．

【解析】

试题分析：（Ⅰ）因为直线过焦点，所以设直线，与抛物线方程联立，转化为，利用焦点弦长公式，，解得直线方程；

（Ⅱ）设，用坐标表示直线的斜率，若成等差数列，那么,代入（1）的坐标后，若恒成立，解得点的坐标.

试题解析：（Ⅰ）焦点∵直线的斜率不为，所以设，

， 由得，

，，

，，

∴， ∴． ∴直线的斜率，

∵，∴， ∴直线的方程为．

（Ⅱ）设，，

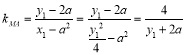同理，，

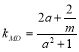∵直线，，的斜率始终成等差数列，

∴恒成立，

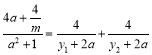即恒成立．

∴，

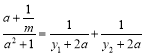
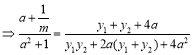把，代入上式，得恒成立，．

∴存在点或，使得对任意直线，直线，，的斜率始终成等差数列．