题目内容
已知函数f(x)=lg(x2+ax-a-1)(a∈R),给出下列命题:①f(x)有最小值;②当a=0时,f(x)的值域为R;③a=1时,f(x)的定义域为(-1,0);④若f(x)在区间[2,+∞)上是增函数,则实数a的取值范围是[-4,+∞).其中正确结论的序号是 .(填上所有正确命题的序号).
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:根据如果x2+ax-a-1<0有解,可判断函数f(x)=lg(x2+ax-a-1)(a∈R),的值域为R,无最小值,
②当a=0时求出值域为R,③a=1时,得出定义域:(-∞,-2)∪(1,+∞),④运用求解
即可.
②当a=0时求出值域为R,③a=1时,得出定义域:(-∞,-2)∪(1,+∞),④运用求解
|
解答:
解:∵函数f(x)=lg(x2+ax-a-1)(a∈R),
∴①如果x2+ax-a-1<0有解,
则函数f(x)=lg(x2+ax-a-1)(a∈R),的值域为R,无最小值,故①不正确,
②当a=0时,函数f(x)=lg(x2-1)(a∈R),定义域为(-∞,-1)∪(1,+∞),值域为R,
故②正确.
③a=1时,f(x)的定义域为:(-∞,-2)∪(1,+∞),故③不正确.
④若f(x)在区间[2,+∞)上是增函数,则
解得:a>-3,
故④不正确,
故答案为:②
∴①如果x2+ax-a-1<0有解,
则函数f(x)=lg(x2+ax-a-1)(a∈R),的值域为R,无最小值,故①不正确,
②当a=0时,函数f(x)=lg(x2-1)(a∈R),定义域为(-∞,-1)∪(1,+∞),值域为R,
故②正确.
③a=1时,f(x)的定义域为:(-∞,-2)∪(1,+∞),故③不正确.
④若f(x)在区间[2,+∞)上是增函数,则
|
故④不正确,
故答案为:②
点评:本题考查了函数的性质,不等式考查定义域,值域问题,属于中档题,难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

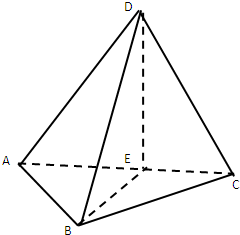 如图,三棱锥D-ABC中,AB=BC=2,BD=3,∠ABC=∠DBA=∠DBC=60°,E为AC的中点.
如图,三棱锥D-ABC中,AB=BC=2,BD=3,∠ABC=∠DBA=∠DBC=60°,E为AC的中点.