题目内容
函数f(x)=
的定义域为 ．
| x |
| ln(x-2) |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据分母不为0，对数的性质得关于x的不等式，解出即可．
解答：
解：要使函数有意义，x应满足：
，
解得x＞2且x≠3，
故函数的定义域为：{x|2＜x＜3或x＞3}；
故答案：{x|2＜x＜3或x＞3}．
|
解得x＞2且x≠3，
故函数的定义域为：{x|2＜x＜3或x＞3}；
故答案：{x|2＜x＜3或x＞3}．
点评：本题考查了分式函数的性质，利用对数的性质求函数的定义域，是一道基础题．
练习册系列答案
相关题目
某小学教师准备购买一些签字笔和铅笔盒作为奖品，已知签字笔每支5元，铅笔盒每个6元，花费总额不能超过50元．为了便于学生选择，购买签字笔和铅笔盒的个数均不能少于3个，那么该教师有 种不同的购买奖品方案．
已知
=（-2，0），
=（0，2）（O为坐标原点），点C在曲线
（θ为参数）上运动，则△ABC面积的最大值为（ ）
| OA |
| OB |
|
A、3-
| ||||
B、3+
| ||||
C、
| ||||
D、
|
设2x=5y=m，且
+
=2，则m的值是（ ）
| 1 |
| x |
| 1 |
| y |
A、±
| ||
B、
| ||
| C、10 | ||
| D、100 |
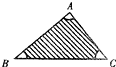△ABC中，AB=8，AC=6，BC=10，顶点A、B、C处分别有一枚半径为1的硬币（顶点A、B、C分别与硬币的中心重合）．向△ABC内部投一点，那么该点落在阴影部分的概率为（ ）A、1-
| ||
B、1-
| ||
C、
| ||
D、
|