题目内容
14．若函数$y=\frac{x-b}{x+2}$在（a，a+6）（b＜-2）上的值域为（2，+∞），则a+b=-10．分析 把已知函数解析式化简，得到$y=1-\frac{b+2}{x+2}$在（a，a+6）上为减函数，由此求得a=-2，在结合函数的单调性可知f（4）=1-$\frac{b+2}{4+2}$=2，求出b后得答案．
解答 解：由$y=\frac{x-b}{x+2}$=$\frac{x+2-b-2}{x+2}=1-\frac{b+2}{x+2}$，
∵b＜-2，∴-（b+2）＞0，
则函数$y=1-\frac{b+2}{x+2}$在（-∞，-2），（-2，+∞）上为减函数，
又函数在（a，a+6）上为减函数，且值域为（2，+∞），
∴a=-2，且f（4）=1-$\frac{b+2}{4+2}$=2，解得：b=-8．
∴a+b=-10．
故答案为：-10．
点评 本题考查函数值域的求法，训练了利用函数单调性求函数的值域，是中档题．
练习册系列答案
口算题天天练系列答案
相关题目
4．中心为原点，一个焦点为$F（0，5\sqrt{2}）$的椭圆截直线y=3x-2所得的弦的中点的横坐标为$\frac{1}{2}$，则椭圆的方程为（ ）
| A． | $\frac{x^2}{25}+\frac{y^2}{75}=1$ | B． | $\frac{x^2}{75}+\frac{y^2}{25}=1$ | C． | $\frac{{2{x^2}}}{75}+\frac{{2{y^2}}}{25}=1$ | D． | $\frac{{2{x^2}}}{25}+\frac{{2{y^2}}}{75}=1$ |
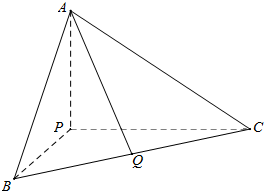在三棱锥P-ABC中，已知PA，PB，PC两两垂直，PB=5，PC=6，三棱锥P-ABC的体积为20，Q是BC的中点，求异面直线PB，AQ所成角的大小（结果用反三角函数值表示）．
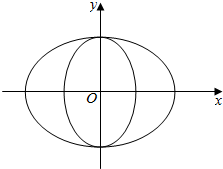如图，曲线Γ由两个椭圆T1：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$和椭圆T2：$\frac{y^2}{b^2}+\frac{x^2}{c^2}=1（{b＞c＞0}）$组成，当a，b，c成等比数列时，称曲线Γ为“猫眼曲线”．
9．下面的命题中是真命题的是（ ）
| A． | 两个平面的法向量所成的角是这两个平面所成的角 | |
| B． | 设空间向量$\overrightarrow a$，$\overrightarrow b$为非零向量，若$\overrightarrow a•\overrightarrow b＞0$，则$＜\overrightarrow a，\overrightarrow b＞$为锐角 | |
| C． | 方程mx2+ny2=1（m＞0，n＞0）表示的曲线是椭圆 | |
| D． | 等轴双曲线的渐近线互相垂直，离心率等于$\sqrt{2}$ |