题目内容
19.将函数$y=sin(ωx+φ)({ω>0,φ∈({-\frac{π}{2},\frac{π}{2}})})$的图象向左平移$\frac{π}{3ω}$个单位后,所得的图象关于y轴对称,则φ的值$\frac{π}{6}$.分析 求得y=sin(ωx+φ)的图象向左平移$\frac{π}{3ω}$个单位后的解析式,利用正弦函数的对称性可得φ的值.
解答 解:∵y=sin(ωx+φ)的图象向左平移$\frac{π}{3ω}$个单位后得:
y=f(x+$\frac{π}{3ω}$)=sin[ω(x+$\frac{π}{3ω}$)+φ)=sin(ωx$+\frac{π}{3}$+φ),
∵y=sin(ωx$+\frac{π}{3}$+φ)的图象关于y轴对称,
∴y=sin(ωx$+\frac{π}{3}$+φ)为偶函数,
∴$\frac{π}{3}$+φ=kπ+$\frac{π}{2}$,k∈Z,
∴φ∈(-$\frac{π}{2}$,$\frac{π}{2}$).
∴φ=$\frac{π}{6}$.
故答案为:$\frac{π}{6}$.
点评 本题考查函数y=Asin(ωx+φ)的图象变换,求得函数图象平移后的解析式是关键,考查综合分析与运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
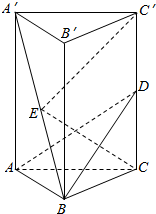 如图,在正三棱柱ABC-A′B′C′中,D、E分别为CC′,A′B中点,CC′=$\sqrt{3}BC$.求证:
如图,在正三棱柱ABC-A′B′C′中,D、E分别为CC′,A′B中点,CC′=$\sqrt{3}BC$.求证: