题目内容
6.已知函数f(x)=x2-2|x|+1,g(x)=-x2+bx+b-5,若g(f(x))=0恰好有5个不同的解,则g(x)≤0的解集为(-∞,1]∪[2,+∞).分析 作出函数f(x)的图象,利用换元法,结合一元二次函数的图象和性质,求出b的值,结合一元二次不等式的解法进行求解即可.
解答 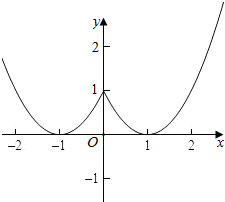 解:作出函数f(x)的图象如图:
解:作出函数f(x)的图象如图:
设t=f(x),
则当t=0或t>1时,t=f(x)有两个不同的根,
当t=1时,t=f(x)有3个不同的根,
若g(f(x))=0恰好有5个不同的解,
则等价为g(t)=0有两个不同的根,其中一根为t=1,
即g(1)=-1+b+b-5=2b-6=0,
得b=3,
此时g(x)=-x2+3x-2,
由g(x)≤0得-x2+3x-2≤0,
即x2-3x+2≥0,
解得x≥2或x≤1,
即不等式的解集为(-∞,1]∪[2,+∞),
故答案为:(-∞,1]∪[2,+∞)
点评 本题主要考查根的存在性的应用,利用换元法结合一元二次函数的性质,一元二次不等式的解法是解决本题的关键.注意要利用数形结合.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
16.圆x2+y2+2x+3y+1=0与圆x2+y2+4x+3y+2=0的位置关系是( )
| A. | 外切 | B. | 内切 | C. | 相交 | D. | 内含 |
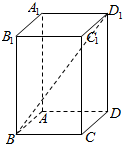 如图,在正四棱柱中ABCD-A1B1C1D1,AB=1,D1B和平面ABCD所成的角的大小为$arctan\frac{{3\sqrt{2}}}{4}$,求该四棱柱的表面积.
如图,在正四棱柱中ABCD-A1B1C1D1,AB=1,D1B和平面ABCD所成的角的大小为$arctan\frac{{3\sqrt{2}}}{4}$,求该四棱柱的表面积.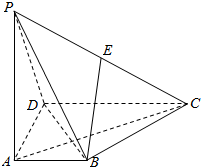 如图,在四棱锥P-ABCD中,PA⊥ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
如图,在四棱锥P-ABCD中,PA⊥ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.