题目内容
已知函数f(x)=(x-2)ex和g(x)=kx3-x-2
(1)若函数g(x)在区间(1,2)不单调,求k的取值范围;
(2)当x∈[0,+∞)时,不等式f(x)≥g(x)恒成立,求k的最大值.
(1)若函数g(x)在区间(1,2)不单调,求k的取值范围;
(2)当x∈[0,+∞)时,不等式f(x)≥g(x)恒成立,求k的最大值.
考点:导数在最大值、最小值问题中的应用,函数单调性的性质,函数恒成立问题
专题:导数的综合应用
分析:(1)求出g'(x)=3kx2-1,通过①当k≤0时,②当k>0时,函数g(x)在区间(1,2)不单调,判断导数的符号,得到函数有极值,即可求k的取值范围;
(2)构造h(x)=f(x)-g(x)=(x-2)ex-kx3+x+2,转化h(x)=(x-2)ex-kx3+x+2≥0在[0,+∞)上恒成立,通过h'(0)=0,对k≤
时,k>
时,判断函数的单调性,以及函数的最值,是否满足题意,求出k的最大值.
(2)构造h(x)=f(x)-g(x)=(x-2)ex-kx3+x+2,转化h(x)=(x-2)ex-kx3+x+2≥0在[0,+∞)上恒成立,通过h'(0)=0,对k≤
| 1 |
| 6 |
| 1 |
| 6 |
解答:
解:(1)g'(x)=3kx2-1…(1分)
①当k≤0时,g'(x)=3kx2-1≤0,所以g(x)在(1,2)单调递减,不满足题意;…(2分)
②当k>0时,g(x)在(0,
)上单调递减,在(
,+∞)上单调递增,
因为函数g(x)在区间(1,2)不单调,所以1<
<2,解得
<k<
…(4分)
综上k的取值范围是
<k<
.…(5分)
(2)令h(x)=f(x)-g(x)=(x-2)ex-kx3+x+2
依题可知h(x)=(x-2)ex-kx3+x+2≥0在[0,+∞)上恒成立 …(6分)
h'(x)=(x-1)ex-3kx2+1,令φ(x)=h'(x)=(x-1)ex-3kx2+1,
有φ(0)=h'(0)=0且φ'(x)=x(ex-6k)…(7分)
①当6k≤1,即k≤
时,
因为x≥0,ex≥1,所以φ'(x)=x(ex-6k)≥0
所以函数φ(x)即h'(x)在[0,+∞)上单调递增,又由φ(0)=h'(0)=0
故当x∈[0,+∞)时,h'(x)≥h'(0)=0,所以h(x)在[0,+∞)上单调递增
又因为h(0)=0,所以h(x)≥0在[0,+∞)上恒成立,满足题意;…(10分)
②当6k>1,即k>
时,
当x∈(0,ln(6k)),φ'(x)=x(ex-6k)<0,函数φ(x)即h'(x)单调递减,
又由φ(0)=h'(0)=0,所以当x∈(0,ln(6k)),h'(x)<h'(0)=0
所以h(x)在(0,ln(6k))上单调递减,又因为h(0)=0,所以x∈(0,ln(6k))时h(x)<0,
这与题意h(x)≥0在[0,+∞)上恒成立相矛盾,故舍.…(13分)
综上k≤
,即k的最大值是
.…(14分)
①当k≤0时,g'(x)=3kx2-1≤0,所以g(x)在(1,2)单调递减,不满足题意;…(2分)
②当k>0时,g(x)在(0,
|
|
因为函数g(x)在区间(1,2)不单调,所以1<
|
| 1 |
| 12 |
| 1 |
| 3 |
综上k的取值范围是
| 1 |
| 12 |
| 1 |
| 3 |
(2)令h(x)=f(x)-g(x)=(x-2)ex-kx3+x+2
依题可知h(x)=(x-2)ex-kx3+x+2≥0在[0,+∞)上恒成立 …(6分)
h'(x)=(x-1)ex-3kx2+1,令φ(x)=h'(x)=(x-1)ex-3kx2+1,
有φ(0)=h'(0)=0且φ'(x)=x(ex-6k)…(7分)
①当6k≤1,即k≤
| 1 |
| 6 |
因为x≥0,ex≥1,所以φ'(x)=x(ex-6k)≥0
所以函数φ(x)即h'(x)在[0,+∞)上单调递增,又由φ(0)=h'(0)=0
故当x∈[0,+∞)时,h'(x)≥h'(0)=0,所以h(x)在[0,+∞)上单调递增
又因为h(0)=0,所以h(x)≥0在[0,+∞)上恒成立,满足题意;…(10分)
②当6k>1,即k>
| 1 |
| 6 |
当x∈(0,ln(6k)),φ'(x)=x(ex-6k)<0,函数φ(x)即h'(x)单调递减,
又由φ(0)=h'(0)=0,所以当x∈(0,ln(6k)),h'(x)<h'(0)=0
所以h(x)在(0,ln(6k))上单调递减,又因为h(0)=0,所以x∈(0,ln(6k))时h(x)<0,
这与题意h(x)≥0在[0,+∞)上恒成立相矛盾,故舍.…(13分)
综上k≤
| 1 |
| 6 |
| 1 |
| 6 |
点评:本题考查函数的导数的综合应用,构造法以及转化思想的应用,同时考查分类讨论思想的应用,难度比较大,考查分析问题解决问题的能力.

练习册系列答案
相关题目
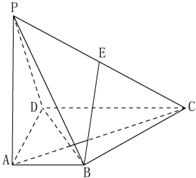 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.