题目内容
3.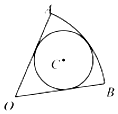 如图,圆C内切于扇形AOB,$∠AOB=\frac{π}{3}$,若在扇形AOB内任取一点,则该点在圆C内的概率为$\frac{2}{3}$.
如图,圆C内切于扇形AOB,$∠AOB=\frac{π}{3}$,若在扇形AOB内任取一点,则该点在圆C内的概率为$\frac{2}{3}$.
分析 本题是一个等可能事件的概率,试验发生包含的事件对应的包含的事件对应的是扇形AOB,满足条件的事件是圆,根据题意,构造直角三角形求得扇形的半径与圆的半径的关系,进而根据面积的求法求得扇形OAB的面积与⊙C的面积比.
解答  解:由题意知本题是一个等可能事件的概率,设圆C的半径为r,
解:由题意知本题是一个等可能事件的概率,设圆C的半径为r,
试验发生包含的事件对应的是扇形AOB,
满足条件的事件是圆,其面积为⊙C的面积=π•r2,
连接OC,延长交扇形于P.
由于CE=r,∠BOP=$\frac{π}{6}$,OC=2r,OP=3r,
则S扇形AOB=$\frac{π•(3r)^{2}}{6}$=$\frac{3π{r}^{2}}{2}$,
∴⊙C的面积与扇形OAB的面积比是$\frac{2}{3}$.
∴概率P=$\frac{2}{3}$,
故答案为$\frac{2}{3}$.
点评 本题是一个等可能事件的概率,对于这样的问题,一般要通过把试验发生包含的事件同集合结合起来,根据集合对应的图形做出面积,用面积的比值得到结果.连接圆心和切点是常用的辅助线做法,本题的关键是求得扇形半径与圆半径之间的关系.

练习册系列答案
相关题目
14.在空间直角坐标系中,点A(1,-2,3)与点B(-1,-2,-3)关于( )对称.
| A. | x轴 | B. | y轴 | C. | z轴 | D. | 原点 |
11.已知数列{an}的前n项和为Sn,且${a_1}=1,{S_n}=\frac{{({n+1}){a_n}}}{2}$,则a2017=( )
| A. | 2016 | B. | 2017 | C. | 4032 | D. | 4034 |
18.下列说法正确的是( )
| A. | 若l∥α,l∥β,则α∥β | B. | 若l∥α,l⊥β,则α⊥β | C. | 若l⊥α,α⊥β,则l∥β | D. | 若l∥α,α⊥β,则l⊥β |
12.已知A、B、C是圆O上的三个点,CO的延长线与线段BA的延长线交于圆外一点.若$\overrightarrow{OC}=m\overrightarrow{OA}+n\overrightarrow{OB}$,其中m,n∈R.则m+n的取值范围是( )
| A. | (0,1) | B. | (-1,0) | C. | (1,+∞) | D. | (-∞,-1) |
