题目内容
6.已知$\vec a=(2cosx,\sqrt{3}cosx)$,$\vec b=(cosx,2sinx)$,函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$(x∈R)(1)求函数f(x)的周期;
(2)若方程f(x)-t=1在$x∈[0,\frac{π}{2}]$内恒有两个不相等的实数解,求实数t的取值范围.
分析 (1)首先利用三角函数的恒等变换,变形成正弦型函数进一步利用函数周期的定义.
(2)把求方程的解得问题转化成求函数的交点问题,进一步利用函数的性质求参数的取值范围
解答 解:(1)$f(x)=2{cos^2}x+\sqrt{3}sin2x$=$cos2x+\sqrt{3}sin2x+1$=$2sin({2x+\frac{π}{6}})+1$,
∴周期T=π;
(2)依题意:由$2sin({2x+\frac{π}{6}})+1$=t+1,得$t=2sin({2x+\frac{π}{6}})$,
即函数y=t与$y=2sin({2x+\frac{π}{6}})$的图象在$x∈[0,\frac{π}{2}]$有两个交点,
∵$x∈[0,\frac{π}{2}]$,∴$2x+\frac{π}{6}∈[\frac{π}{6},\frac{7π}{6}]$.
当$2x+\frac{π}{6}∈[\frac{π}{6},\frac{π}{2}]$时,$sin({2x+\frac{π}{6}})∈[\frac{1}{2},1]$,y∈[1,2]
当$2x+\frac{π}{6}∈[\frac{π}{2},\frac{7π}{6}]$时,$sin({2x+\frac{π}{6}})∈[-\frac{1}{2},1]$,y∈[-1,2]
故由正弦图象得:1≤t<2
点评 本题考查的知识要点:三角函数的恒等变换,正弦型函数的单调性,在同一坐标系内的利用两函数的交点问题求参数的取值范围问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16. 如图,矩形AnBnCnDn的一边AnBn在x轴上,另外两个顶点Cn,Dn在函数f(x)=x+$\frac{1}{2x}({x>0})$的图象上.若点Bn的坐标为(n,0)(n∈N*),记矩形AnBnCnDn的周长为an,则a1+a2+…+a10( )
如图,矩形AnBnCnDn的一边AnBn在x轴上,另外两个顶点Cn,Dn在函数f(x)=x+$\frac{1}{2x}({x>0})$的图象上.若点Bn的坐标为(n,0)(n∈N*),记矩形AnBnCnDn的周长为an,则a1+a2+…+a10( )
 如图,矩形AnBnCnDn的一边AnBn在x轴上,另外两个顶点Cn,Dn在函数f(x)=x+$\frac{1}{2x}({x>0})$的图象上.若点Bn的坐标为(n,0)(n∈N*),记矩形AnBnCnDn的周长为an,则a1+a2+…+a10( )
如图,矩形AnBnCnDn的一边AnBn在x轴上,另外两个顶点Cn,Dn在函数f(x)=x+$\frac{1}{2x}({x>0})$的图象上.若点Bn的坐标为(n,0)(n∈N*),记矩形AnBnCnDn的周长为an,则a1+a2+…+a10( )| A. | 208 | B. | 212 | C. | 216 | D. | 220 |
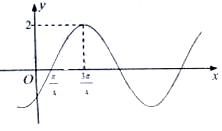
17.已知函数$f(x)=2sin({ωx+φ})({ω>0,-\frac{π}{2}<φ<\frac{π}{2}})$的部分图象如图所示,则下列结论错误的是( )

| A. | $φ=-\frac{π}{4}$ | |
| B. | 函数f(x)在$[{-\frac{π}{4},\frac{3π}{4}}]$上单调递增 | |
| C. | 函数f(x)的一条对称轴是$x=\frac{3π}{4}$ | |
| D. | 为了得到函数f(x)的图象,只需将函数y=2cosx的图象向右平移$\frac{π}{4}$个单位 |
14.在空间直角坐标系中,点A(1,-2,3)与点B(-1,-2,-3)关于( )对称.
| A. | x轴 | B. | y轴 | C. | z轴 | D. | 原点 |
1.已知f(x)=$\frac{lnx}{x}$,若f′(x0)=0,则x0=( )
| A. | e2 | B. | e | C. | 1 | D. | ln2 |
11.已知数列{an}的前n项和为Sn,且${a_1}=1,{S_n}=\frac{{({n+1}){a_n}}}{2}$,则a2017=( )
| A. | 2016 | B. | 2017 | C. | 4032 | D. | 4034 |
18.下列说法正确的是( )
| A. | 若l∥α,l∥β,则α∥β | B. | 若l∥α,l⊥β,则α⊥β | C. | 若l⊥α,α⊥β,则l∥β | D. | 若l∥α,α⊥β,则l⊥β |
 某班级将从甲、乙两位同学中选派一人参加数学竞赛,老师对他们平时的5次模拟测试成绩(满分:100分)进行了记录,其统计数据的茎叶图如图所示,已知甲、乙两位同学的平均成绩都为90分.
某班级将从甲、乙两位同学中选派一人参加数学竞赛,老师对他们平时的5次模拟测试成绩(满分:100分)进行了记录,其统计数据的茎叶图如图所示,已知甲、乙两位同学的平均成绩都为90分.