已知正四棱柱(底面是正方形.侧棱垂直于底面)的高为4.体积为16.八个顶点都在一个球面上.则这个球的表面积是24π．题目和参考答案——青夏教育精英家教网——

题目内容

2．已知正四棱柱（底面是正方形，侧棱垂直于底面）的高为4，体积为16，八个顶点都在一个球面上，则这个球的表面积是24π．

分析先求正四棱柱的底面边长，然后求其对角线，就是球的直径，再求其表面积．

解答解：正四棱柱高为4，体积为16，底面积为4，正方形边长为2，
正四棱柱的对角线长即球的直径为2$\sqrt{6}$，
∴球的半径为$\sqrt{6}$，球的表面积是24π，
故答案为．

点评本题考查学生空间想象能力，四棱柱的体积，球的表面积，容易疏忽的地方是几何体的体对角线是外接球的直径，导致出错．

练习册系列答案

暑假高效作业系列答案

惠宇文化同步学典系列答案

小学零距离期末暑假衔接系列答案

快乐假期培优衔接暑假电子科技大学出版社系列答案

新思维新世界新假期我的暑假我做主系列答案

暑假生活新疆教育出版社系列答案

钟书金牌暑假作业吉林教育出版社系列答案

暑假作业深圳报业集团出版社系列答案

暑假生活四川大学出版社系列答案

Happy holiday快乐假期寒电子科技大学出版社系列答案

相关题目

12．已知实数x，y满足$\left\{\begin{array}{l}2x-y+4≥0\\ x-2y-5≤0\\ x+2y-4≤0\end{array}\right.$，则z=2x+3y的最大值与最小值之差为（　　）

-$\frac{68}{3}$

$\frac{371}{12}$

13．已知函数f_k（x）=a^x+ka^-x，（k∈Z，a＞0且a≠1）．
（Ⅰ）若f₁（1）=3，求f₁（$\frac{1}{2}$）的值；
（Ⅱ）若f_k（x）为定义在R上的奇函数，且a＞1，是否存在实数λ，使得f_k（cos2x）+f_k（2λsinx-5）＜0对任意x∈[0，$\frac{2π}{3}$]恒成立，若存在，请求出实数k的取值范围；若不存在，请说明理由．

10．若${（{1-2x}）^{2013}}={a_0}+{a_1}x+…+{a_{2013}}{x^{2013}}（{x∈R}）$，则$\frac{a_1}{2^2}+\frac{a_2}{2^3}+…+\frac{{{a_{2013}}}}{{{2^{2014}}}}$值为（　　）

17．已知函数$f（x）=2sin（{ωx+φ}）（{ω＞0，-\frac{π}{2}＜φ＜\frac{π}{2}}）$的部分图象如图所示，则下列结论错误的是（　　）

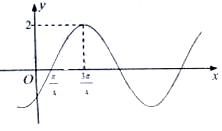
	A．	$φ=-\frac{π}{4}$
	B．	函数f（x）在$[{-\frac{π}{4}，\frac{3π}{4}}]$上单调递增
	C．	函数f（x）的一条对称轴是$x=\frac{3π}{4}$
	D．	为了得到函数f（x）的图象，只需将函数y=2cosx的图象向右平移$\frac{π}{4}$个单位

7．（1）利用“五点法”画出函数$f（x）=sin（\frac{1}{2}x+\frac{π}{6}）$在$[{-\frac{π}{3}，\frac{11π}{3}}]$内的简图

x
$\frac{1}{2}$x+$\frac{π}{6}$
y

（2）若对任意x∈[0，2π]，都有f（x）-3＜m＜f（x）+3恒成立，求m的取值范围．

14．在空间直角坐标系中，点A（1，-2，3）与点B（-1，-2，-3）关于（　　）对称．

11．已知数列{a_n}的前n项和为S_n，且${a_1}=1，{S_n}=\frac{{（{n+1}）{a_n}}}{2}$，则a₂₀₁₇=（　　）

12．已知A、B、C是圆O上的三个点，CO的延长线与线段BA的延长线交于圆外一点．若$\overrightarrow{OC}=m\overrightarrow{OA}+n\overrightarrow{OB}$，其中m，n∈R．则m+n的取值范围是（　　）

（-∞，-1）