题目内容
3.在△ABC中,角A,B,C所对的边分别为a,b,c,满足$\frac{cosB}{cosC}+\frac{2a}{c}+\frac{b}{c}=0$.(Ⅰ)求∠C的大小;
(Ⅱ)求sin2A+sin2B的取值范围.
分析 (Ⅰ)利用正弦定理将边化角,结合和与差的公式可得∠C的大小.
(Ⅱ)降次后利用辅助角公式转化为三角函数,利用三角函数的有界限即可得取值范围.
解答 解:(Ⅰ)在△ABC中,∵$\frac{cosB}{cosC}+\frac{2a}{c}+\frac{b}{c}=0$,
∴由正弦定理可得:$\frac{cosB}{cosC}+\frac{2sinA}{sinC}+\frac{sinB}{sinC}=0$,
∴sinCcosB+sinBcosC+2sinAcosC=0,
∴sinA+2sinAcosC=0,
∵sinA≠0,
∴$cosC=-\frac{1}{2}$,
∵0<C<π.
∴$C=\frac{2π}{3}$.
(Ⅱ)∵${sin^2}A+{sin^2}B=1-\frac{cos2A+cos2B}{2}=1-\frac{1}{2}sin(2A+\frac{π}{6})$,
又∵$0<A<\frac{π}{3}$,
∴$\frac{π}{6}<2A+\frac{π}{6}<\frac{5π}{6}$,
∴$\frac{1}{2}<sin(2A+\frac{π}{6})≤1$,
即${sin^2}A+{sin^2}B∈[\frac{1}{2},\frac{3}{4})$.
故得sin2A+sin2B的取值范围是[$\frac{1}{2}$,$\frac{3}{4}$).
点评 本题考查三角形的正弦定理的运用以及二倍角,辅助角公式的化解能力,考查运算能力,属于基础题.

练习册系列答案
相关题目
13.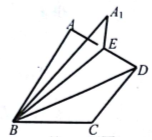 如图,在直二面角A-BD-C中,△ABD、△CBD均是以BD为斜边的等腰直角三角形,取AD中点E,将△ABE沿BE翻折到△A1BE,在△ABE的翻折过程中,下列不可能成立的是( )
如图,在直二面角A-BD-C中,△ABD、△CBD均是以BD为斜边的等腰直角三角形,取AD中点E,将△ABE沿BE翻折到△A1BE,在△ABE的翻折过程中,下列不可能成立的是( )
 如图,在直二面角A-BD-C中,△ABD、△CBD均是以BD为斜边的等腰直角三角形,取AD中点E,将△ABE沿BE翻折到△A1BE,在△ABE的翻折过程中,下列不可能成立的是( )
如图,在直二面角A-BD-C中,△ABD、△CBD均是以BD为斜边的等腰直角三角形,取AD中点E,将△ABE沿BE翻折到△A1BE,在△ABE的翻折过程中,下列不可能成立的是( )| A. | BC与平面A1BE内某直线平行 | B. | CD∥平面A1BE | ||
| C. | BC与平面A1BE内某直线垂直 | D. | BC⊥A1B |