题目内容
下面有五个命题
①函数f（x）=sin4x-cos4x图象的一个对称中心是(-
，0)；
②y=
的图象关于点（-1，1）对称，
③关于x的方程x2+（a+1）x+a+b+1=0（a≠0，a、b∈R）的两实根为x1，x2，若0＜x1＜1＜x2＜2，则
的取值范围是（-
，-
）
④设f（x）是连续的偶函数，且在（0，+∞）是单调函数，则方程f(x)=f(
)所有根之和为8
⑤不等式sinx＞
对任意x∈(0，
)恒成立．
其中真命题的序号是 ．
①函数f（x）=sin4x-cos4x图象的一个对称中心是(-
| π |
| 4 |
②y=
| x+3 |
| x-1 |
③关于x的方程x2+（a+1）x+a+b+1=0（a≠0，a、b∈R）的两实根为x1，x2，若0＜x1＜1＜x2＜2，则
| b |
| a |
| 5 |
| 4 |
| 1 |
| 2 |
④设f（x）是连续的偶函数，且在（0，+∞）是单调函数，则方程f(x)=f(
| x+3 |
| x+4 |
⑤不等式sinx＞
| 4x2 |
| π2 |
| π |
| 2 |
其中真命题的序号是
考点：命题的真假判断与应用
专题：计算题,阅读型,函数的性质及应用,三角函数的图像与性质
分析：运用二倍角的余弦公式，化简f（x），再由余弦函数的对称中心，即可判断①；
由反比例函数的图象的对称性，以及图象平移的规律，即可判断②；
由二次方程实根的分布，结合二次函数的图象，得到不等式组，画出可行域，再由直线的斜率公式，即可判断③；
运用偶函数的性质和单调性，结合韦达定理，即可判断④；
运用正弦函数和抛物线的图象，即可判断⑤．
由反比例函数的图象的对称性，以及图象平移的规律，即可判断②；
由二次方程实根的分布，结合二次函数的图象，得到不等式组，画出可行域，再由直线的斜率公式，即可判断③；
运用偶函数的性质和单调性，结合韦达定理，即可判断④；
运用正弦函数和抛物线的图象，即可判断⑤．
解答：
解：对于①，函数f（x）=sin4x-cos4x=（sin2x-cos2x）
（sin2x+cos2x）=-cos2x，令2x=kπ+
，即x=
+
，k为整数，即关于（
+
，0）对称，则①对；
对于②，y=
=1+
的图象可由y=
的图象向右平移一个单位，再向上平移一个单位得到，故关于（1，1）对称，
则②错；
对于③，关于x的方程x2+（a+1）x+a+b+1=0（a≠0，
a、b∈R）的两实根为x1，x2，
且0＜x1＜1＜x2＜2，则
即有
，
作出不等式组表示的可行域，
=
表示点（a，b）与原点的斜率，
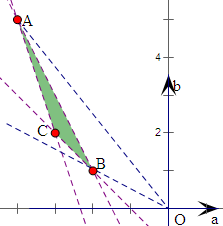
易得A（-4，5），B（-2，1），C（-3，2），kOA=-
，kOB=-
，由图象，
可知
的取值范围是（-
，-
），则③对；
对于④，设f（x）是连续的偶函数，且在（0，+∞）是单调函数，则方程f(x)=f(
)
即为f（|x|）=f（|
|），则有x=
或x+
=0，即有x2+3x-3=0或x2+5x+3=0，
即有韦达定理可得，x1+x2=-3，x3+x4=-5，所有根之和为-8，则④错；
对于⑤，令y=sinx，y=
，则x=0，y=0，x=
，y=1，由sinx在（0，
）的图象上凸，
y=
为抛物线下凹，则不等式sinx＞
对任意x∈(0，
)恒成立．则⑤对．
故答案为：①③⑤
解：对于①，函数f（x）=sin4x-cos4x=（sin2x-cos2x）（sin2x+cos2x）=-cos2x，令2x=kπ+
| π |
| 2 |
| kπ |
| 2 |
| π |
| 4 |
| kπ |
| 2 |
| π |
| 4 |
对于②，y=
| x+3 |
| x-1 |
| 4 |
| x-1 |
| 4 |
| x |
则②错；
对于③，关于x的方程x2+（a+1）x+a+b+1=0（a≠0，
a、b∈R）的两实根为x1，x2，
且0＜x1＜1＜x2＜2，则
|
|
作出不等式组表示的可行域，
| b |
| a |
| b-0 |
| a-0 |
易得A（-4，5），B（-2，1），C（-3，2），kOA=-
| 5 |
| 4 |
| 1 |
| 2 |
可知
| b |
| a |
| 5 |
| 4 |
| 1 |
| 2 |
对于④，设f（x）是连续的偶函数，且在（0，+∞）是单调函数，则方程f(x)=f(
| x+3 |
| x+4 |
即为f（|x|）=f（|
| x+3 |
| x+4 |
| x+3 |
| x+4 |
| x+3 |
| x+4 |
即有韦达定理可得，x1+x2=-3，x3+x4=-5，所有根之和为-8，则④错；
对于⑤，令y=sinx，y=
| 4x2 |
| π2 |
| π |
| 2 |
| π |
| 2 |
y=
| 4x2 |
| π2 |
| 4x2 |
| π2 |
| π |
| 2 |
故答案为：①③⑤
点评：本题考查函数的对称性、二次方程实根的分布和不等式表示的平面区域、函数的奇偶性和运用，以及不等式恒成立问题的解法，考查数形结合的思想方法，属于中档题和易错题．
练习册系列答案
相关题目
已知m，n∈R，则“lnm＜lnn”是“em＜en”的（ ）
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、不充分不必要条件 |
下列不等式中，正确的是（ ）
A、tan
| ||||
B、sin
| ||||
C、sin
| ||||
D、cos
|
设实数x和y满足约束条件
，且z=ax+y取得最小值的最优解仅为点A（1，2），则实数a的取值范围是（ ）
|
A、(-∞，-
| ||
B、(-∞，-
| ||
C、(
| ||
D、[
|
到两定点F1（-3，0）、F2（3，0）的距离之差的绝对值等于6的点M的轨迹（ ）
| A、两条射线 | B、线段 |
| C、双曲线 | D、椭圆 |
下列几何体的三视图是一样的为（ ）
| A、圆台 | B、圆锥 | C、圆柱 | D、球 |