题目内容
已知函数f(x)=ax-1(x≥0)的图象经过点(3,
),其中a>0且a≠1.
(1)求a的值;
(2)若kf2(x)-2f(x)≥-2恒成立,其中x∈(0,2],求k的取值范围.
| 1 |
| 9 |
(1)求a的值;
(2)若kf2(x)-2f(x)≥-2恒成立,其中x∈(0,2],求k的取值范围.
考点:函数恒成立问题,指数函数的单调性与特殊点
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:(1)运用代入法,再解方程,即可得到a;
(2)可用换元法,令t=(
)x,不等式即为9kt2-6t+2≥0恒成立,t∈[
,1),即有9k≥
,对右边配方,求出最大值即可.
(2)可用换元法,令t=(
| 1 |
| 3 |
| 1 |
| 9 |
| 6t-2 |
| t2 |
解答:
解:(1)函数f(x)=ax-1(x≥0)的图象经过点(3,
),
则a2=
,解得,a=
;
(2)f(x)=(
)x-1,kf2(x)-2f(x)≥-2恒成立,
即为k•(
)2x-2-2•(
)x-1≥-2,
令t=(
)x,由于x∈(0,2],则t∈[
,1),
则9kt2-6t+2≥0恒成立,即有9k≥
=-2(
-
)2+
,
由于t∈[
,1),则
∈(1,9],
则当
=
∈(1,9],不等式右边取得最大值
,
则9k≥
,则k≥
.
则k的取值范围是[
,+∞).
| 1 |
| 9 |
则a2=
| 1 |
| 9 |
| 1 |
| 3 |
(2)f(x)=(
| 1 |
| 3 |
即为k•(
| 1 |
| 3 |
| 1 |
| 3 |
令t=(
| 1 |
| 3 |
| 1 |
| 9 |
则9kt2-6t+2≥0恒成立,即有9k≥
| 6t-2 |
| t2 |
| 1 |
| t |
| 3 |
| 2 |
| 9 |
| 2 |
由于t∈[
| 1 |
| 9 |
| 1 |
| t |
则当
| 1 |
| t |
| 3 |
| 2 |
| 9 |
| 2 |
则9k≥
| 9 |
| 2 |
| 1 |
| 2 |
则k的取值范围是[
| 1 |
| 2 |
点评:本题考查指数函数的图象和性质及运用,考查不等式恒成立问题转化为求函数的最值,考查运算能力,属于中档题.

练习册系列答案
相关题目
若集合A={y|y=2x+1},B={x|y=
}则(∁RA)∩B( )
| -x2-x+6 |
| A、[-3,1] |
| B、(-∞,-3) |
| C、[-3,-1) |
| D、(-∞,0) |
设函数f(x)=
的最小值为-1,则实数a取值范围( )
|
A、{a|a≥-
| ||
B、{a|a>-
| ||
C、{a|a<-
| ||
| D、{a|a≥-1} |
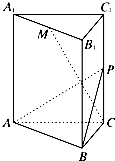 如图,三棱柱ABC-A1B1C1的底面是边长为4正三角形,AA1⊥平面ABC,AA1=2
如图,三棱柱ABC-A1B1C1的底面是边长为4正三角形,AA1⊥平面ABC,AA1=2