题目内容
设实数x和y满足约束条件
,且z=ax+y取得最小值的最优解仅为点A(1,2),则实数a的取值范围是( )
|
A、(-∞,-
| ||
B、(-∞,-
| ||
C、(
| ||
D、[
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出约束条件
所对应的可行域,变形目标函数可得y=-ax+z,其中直线斜率为-a,截距为z,由题意可得-a<-
,解不等式可得.
|
| 1 |
| 3 |
解答:
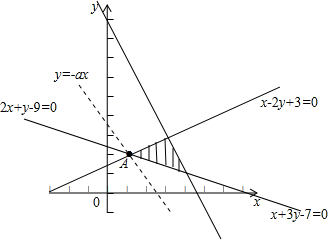 解:作出约束条件
解:作出约束条件
所对应的可行域(如图阴影),
变形目标函数可得y=-ax+z,其中直线斜率为-a,截距为z,
∵z=ax+y取得最小值的最优解仅为点A(1,2),
∴直线的斜率-a<-
,(-
为直线x+3y-7=0的斜率)
解不等式可得a>
,即实数a的取值范围为(
,+∞)
故选:C
 解:作出约束条件
解:作出约束条件
|
变形目标函数可得y=-ax+z,其中直线斜率为-a,截距为z,
∵z=ax+y取得最小值的最优解仅为点A(1,2),
∴直线的斜率-a<-
| 1 |
| 3 |
| 1 |
| 3 |
解不等式可得a>
| 1 |
| 3 |
| 1 |
| 3 |
故选:C
点评:本题考查简单线性规划,准确作图是解决问题的关键,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列命题的说法错误的是( )
| A、若p∧q为假命题,则p,q均为假命题. |
| B、“x=1”是“x2-3x+2=0”的充分不必要条件. |
| C、对于命题p:?x∈R,x2+x+1>0,则?p:?x∈R,x2+x+1≤0. |
| D、命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0” |
已知O为坐标原点,
=(x,y),
=(a,0),
=(0,a),
=(3,4),记|
|、|
|、|
|中的最大值为M,当a取遍一切实数时,M的取值范围是( )
| OP |
| OA |
| OB |
| OC |
| PA |
| PB |
| PC |
A、[
| ||
B、[7+2
| ||
C、[7-2
| ||
D、[7,7+2
|
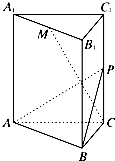 如图,三棱柱ABC-A1B1C1的底面是边长为4正三角形,AA1⊥平面ABC,AA1=2
如图,三棱柱ABC-A1B1C1的底面是边长为4正三角形,AA1⊥平面ABC,AA1=2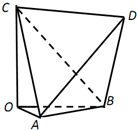 如图,多面体OABCD,AB=CD=2,AD=BC=2
如图,多面体OABCD,AB=CD=2,AD=BC=2