题目内容
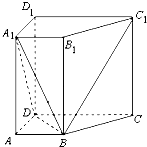 如图,已知在直四棱柱ABCD-A1B1C1D1(侧棱垂直底面的棱柱)中,AD⊥DC,AB∥DC,DC=DD1=2AD=2AB=2.
如图,已知在直四棱柱ABCD-A1B1C1D1(侧棱垂直底面的棱柱)中,AD⊥DC,AB∥DC,DC=DD1=2AD=2AB=2.(1)求证:DB⊥平面B1BCC1;
(2)求BC1与平面A1BD所成的角的正弦值.
考点:直线与平面所成的角,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)首先根据题中的已知条件找到线线垂直,进一步找到线面垂直的条件,来证明线面垂直.
(2)要求直线与平面的夹角,首先找到直线与平面所成角的平面角,然后利用余弦定理来求解.
(2)要求直线与平面的夹角,首先找到直线与平面所成角的平面角,然后利用余弦定理来求解.
解答:

证明:(1)设E是DC的中点,连结BE,则四边形DABE为正方形.
∴BE⊥CD,故BD=
,BC=
,CD=2
∴∠DBC=90°即:BD⊥BC
∵BD⊥BB1 BB1∩BC=B
∴BD⊥平面BCC1B1
(2)由(1)知∴BD⊥平面BCC1B1
BC1?平面BCC1B1
∴BD⊥BC1
取BD的中点F,连结A1F,A1D=A1B
A1F⊥BD
取DC1的中点M,连结FM,
则:FM∥BC1
∴FM⊥BD
∴BD⊥平面A1FM
过M向平面A1FM作垂线,垂足必落在A1F上,
∴∠A1FM为直线BC1与平面A1BD所成的角.
连结A1M,在△A1FM中,A1F=
FM=
BC1=
=
取D1C1的中点H,连结A1H,HM
在Rt△A1HM中,A1H=
,HM=1,A1M=
∴cos∠A1FM=
=
∴直线BC1与平面A1BD所成角的正弦值为

证明:(1)设E是DC的中点,连结BE,则四边形DABE为正方形.
∴BE⊥CD,故BD=
| 2 |
| 2 |
∴∠DBC=90°即:BD⊥BC
∵BD⊥BB1 BB1∩BC=B
∴BD⊥平面BCC1B1
(2)由(1)知∴BD⊥平面BCC1B1
BC1?平面BCC1B1
∴BD⊥BC1
取BD的中点F,连结A1F,A1D=A1B
A1F⊥BD
取DC1的中点M,连结FM,
则:FM∥BC1
∴FM⊥BD
∴BD⊥平面A1FM
过M向平面A1FM作垂线,垂足必落在A1F上,
∴∠A1FM为直线BC1与平面A1BD所成的角.
连结A1M,在△A1FM中,A1F=
| 3 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| BC2+CC12 |
| ||
| 2 |
取D1C1的中点H,连结A1H,HM
在Rt△A1HM中,A1H=
| 2 |
| 3 |
∴cos∠A1FM=
| A1F2+FM2-A1M2 |
| 2A1F•FM |
| ||
| 3 |
∴直线BC1与平面A1BD所成角的正弦值为
| ||
| 3 |
点评:本题考查的知识点:线面垂直的判定,线面垂直的性质定理,直线与平面所成的角,余弦定理勾股定理及相关的运算问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设等差数列{an}的前n项和为Sn.若a5=5a3,则
=( )
| S9 |
| S5 |
| A、10 | B、9 | C、12 | D、5 |
曲线y=
x3+x在点(1,
)处的切线与坐标轴围成的三角形的面积为( )
| 1 |
| 3 |
| 4 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|