题目内容
已知命题P:?x0∈R,ax02+2x0+3≤0,若P为假命题,则a的取值范围是 .
考点:特称命题
专题:简易逻辑
分析:“?x0∈R,使ax02+2x0+3≤0”为假命题,等价于?x∈R,ax2+2x+3>0为真命题,由此可以确定实数a的取值范围.
解答:
解:?x0∈R,使ax02+2x0+3≤0为假命题,等价于?x∈R,ax2+2x+3>0为真命题,
∴a≤0时,不满足题意;
a>0时,△=22-4a×3<0,
解得a>
,
∴实数a的取值范围是{a|a>
}.
故答案为:{a|a>
}.
∴a≤0时,不满足题意;
a>0时,△=22-4a×3<0,
解得a>
| 1 |
| 3 |
∴实数a的取值范围是{a|a>
| 1 |
| 3 |
故答案为:{a|a>
| 1 |
| 3 |
点评:本题通过特称命题与全称命题的关系,考查一元二次不等式的恒成立问题,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知圆上的一段弧长等于该圆的内接正方形的边长,则这段弧所对的圆周角的弧度数为( )
A、
| ||||
B、2
| ||||
C、
| ||||
D、
|
如图所示是计算某年级500名学生期末考试(满分为100分)及格率q的程序框图,则图中空白框内应填入( )
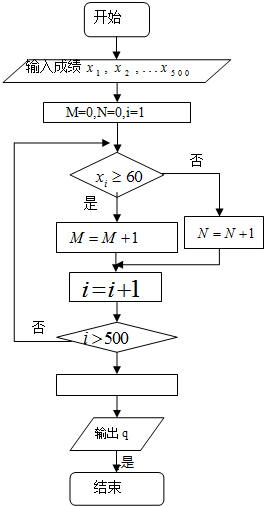

A、q=
| ||
B、q=
| ||
C、q=
| ||
D、q=
|
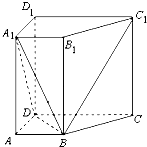 如图,已知在直四棱柱ABCD-A1B1C1D1(侧棱垂直底面的棱柱)中,AD⊥DC,AB∥DC,DC=DD1=2AD=2AB=2.
如图,已知在直四棱柱ABCD-A1B1C1D1(侧棱垂直底面的棱柱)中,AD⊥DC,AB∥DC,DC=DD1=2AD=2AB=2.