题目内容
设双曲线
-
=1(a>0,b>0)的离心率为
,且它的一条准线与抛物线y=
x2的准线重合,则此双曲线的方程为 .
| y2 |
| a2 |
| x2 |
| b2 |
| 3 |
| 1 |
| 4 |
考点:双曲线的标准方程
专题:
分析:求出抛物线y=
x2的准线方程,利用双曲线
-
=1(a>0,b>0)的离心率为
,且它的一条准线与抛物线y=
x2的准线重合,求出a,c可得b,即可求出双曲线的方程
| 1 |
| 4 |
| y2 |
| a2 |
| x2 |
| b2 |
| 3 |
| 1 |
| 4 |
解答:
解:抛物线y=
x2的准线方程为y=-1,
∵双曲线
-
=1(a>0,b>0)的离心率为
,且它的一条准线与抛物线y=
x2的准线重合,
∴
=
,
=1,
∴a=
,c=3,
∴b=
,
∴双曲线的方程为
-
=1,
故答案为:
-
=1.
| 1 |
| 4 |
∵双曲线
| y2 |
| a2 |
| x2 |
| b2 |
| 3 |
| 1 |
| 4 |
∴
| c |
| a |
| 3 |
| a2 |
| c |
∴a=
| 3 |
∴b=
| 6 |
∴双曲线的方程为
| x2 |
| 3 |
| y2 |
| 6 |
故答案为:
| x2 |
| 3 |
| y2 |
| 6 |
点评:本题考查双曲线的标准方程,考查双曲线的几何性质,比较基础.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
已知圆上的一段弧长等于该圆的内接正方形的边长,则这段弧所对的圆周角的弧度数为( )
A、
| ||||
B、2
| ||||
C、
| ||||
D、
|
已知0<a<b,且a+b=1,则下列不等式①log2a>-1;②log2a+log2b>-2;③log2(b-a)<0;④log2(
+
)>1,其中一定成立的不等式的序号是( )
| b |
| a |
| a |
| b |
| A、①② | B、②③ | C、③④ | D、①④ |
如图所示是计算某年级500名学生期末考试(满分为100分)及格率q的程序框图,则图中空白框内应填入( )
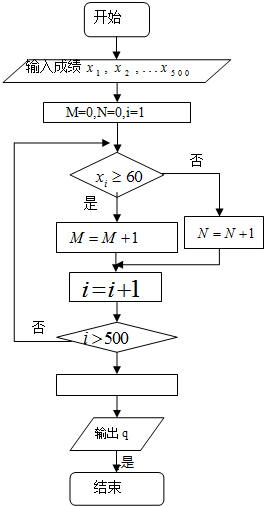

A、q=
| ||
B、q=
| ||
C、q=
| ||
D、q=
|
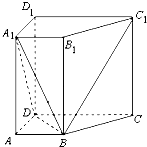 如图,已知在直四棱柱ABCD-A1B1C1D1(侧棱垂直底面的棱柱)中,AD⊥DC,AB∥DC,DC=DD1=2AD=2AB=2.
如图,已知在直四棱柱ABCD-A1B1C1D1(侧棱垂直底面的棱柱)中,AD⊥DC,AB∥DC,DC=DD1=2AD=2AB=2.