题目内容
函数f(x)的定义域为A,若x1,x2∈A且f(x1)=f(x2)时,总有x1=x2,则称f(x)为单函数.例如,函数f(x)=2x+1(x∈R)是单函数.下列命题:
①函数f(x)=x2(x∈R)是单函数;
②若f(x)为单函数,x1,x2∈A且x1≠x2,则f(x1)≠f(x2);
③若f(x)为单函数,则其导函数f′(x)=0无解;
④函数f(x)在某区间上具有单调性,则f(x)一定是单函数.
其中的真命题是 (写出所有真命题的编号).
①函数f(x)=x2(x∈R)是单函数;
②若f(x)为单函数,x1,x2∈A且x1≠x2,则f(x1)≠f(x2);
③若f(x)为单函数,则其导函数f′(x)=0无解;
④函数f(x)在某区间上具有单调性,则f(x)一定是单函数.
其中的真命题是
考点:命题的真假判断与应用
专题:简易逻辑
分析:从给的条件可以看出,单函数的自变量x与函数值y间是一一对应的关系,据此判断:
①举个反例可说明其不是单函数,如令f(x)=1,得x=±1,故①假;
②考虑其逆否命题就是单函数的定义,所以②真;
③举反例,如y=x3,其导函数在x=0处导数为0;
④只有严格单调递增或递减时,才能符合题意是单函数,故④假.
①举个反例可说明其不是单函数,如令f(x)=1,得x=±1,故①假;
②考虑其逆否命题就是单函数的定义,所以②真;
③举反例,如y=x3,其导函数在x=0处导数为0;
④只有严格单调递增或递减时,才能符合题意是单函数,故④假.
解答:
解:对于①,当f(x)=1时,解得x=±1,不满足单函数定义,故①假;
对于②,该命题的逆否命题就是单函数的定义,故②真;
对于③,举例:函数y=x3的导数在x=0时为0,故③为假;
对于④,只有在定义域上严格单调递增或单调递减的函数才是单函数,故④假.
故答案为②.
对于②,该命题的逆否命题就是单函数的定义,故②真;
对于③,举例:函数y=x3的导数在x=0时为0,故③为假;
对于④,只有在定义域上严格单调递增或单调递减的函数才是单函数,故④假.
故答案为②.
点评:此题考查了函数的单调性与单函数间的关系,注意理解单调函数的定义:如函数定义域为[0,2],但该函数在[0,1]为常函数0,在(1,2]上是y=x上一段,此时我们也称该函数为定义域内的单调函数.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
如图所示是计算某年级500名学生期末考试(满分为100分)及格率q的程序框图,则图中空白框内应填入( )
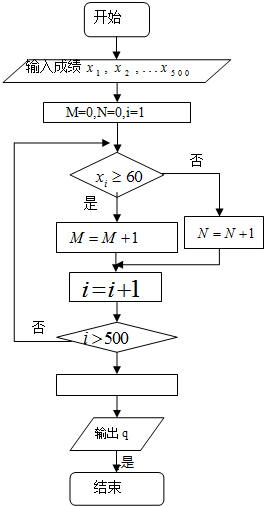

A、q=
| ||
B、q=
| ||
C、q=
| ||
D、q=
|
下列说法正确的是( )
| A、命题“?x0∈R,x02+x0+1<0”的否定是:“?x∈R,x2+x+1>0” |
| B、“x=-1”是“x2-5x-6=0”的必要不充分条件 |
| C、命题“若x2=1,则x=1”的否命题是:若x2=1,则x≠1 |
| D、命题“若x=y,则sin x=sin y”的逆否命题为真命题 |
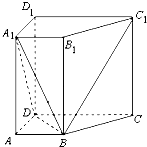 如图,已知在直四棱柱ABCD-A1B1C1D1(侧棱垂直底面的棱柱)中,AD⊥DC,AB∥DC,DC=DD1=2AD=2AB=2.
如图,已知在直四棱柱ABCD-A1B1C1D1(侧棱垂直底面的棱柱)中,AD⊥DC,AB∥DC,DC=DD1=2AD=2AB=2.