题目内容
求曲线y=x3的过(1,1)的切线方程.
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:①若(1,1)为切点,根据导数的几何意义求出函数f(x)在x=2处的导数,从而求出切线的斜率,再用点斜式写出切线方程;
②若不是切点,设出切点坐标,求出切线的斜率,由点斜式写出切线方程,把原点代入切线方程中化简可求出切点的横坐标,把横坐标代入即可求出切点的纵坐标,且得到切线的斜率,即可求出切线方程.
②若不是切点,设出切点坐标,求出切线的斜率,由点斜式写出切线方程,把原点代入切线方程中化简可求出切点的横坐标,把横坐标代入即可求出切点的纵坐标,且得到切线的斜率,即可求出切线方程.
解答:
解:y=x3的导数y′=3x2,
①若(1,1)为切点,k=3•12=3,
∴切线l:y-1=3(x-1)即3x-y-2=0;
②若(1,1)不是切点,
设切点P(m,m3),k=3m2=
,
即2m2-m-1=0,则m=1(舍)或-
∴切线l:y-1=
(x-1)即3x-4y+1=0.
故切线方程为:3x-y-2=0或3x-4y+1=0.
①若(1,1)为切点,k=3•12=3,
∴切线l:y-1=3(x-1)即3x-y-2=0;
②若(1,1)不是切点,
设切点P(m,m3),k=3m2=
| m3-1 |
| m-1 |
即2m2-m-1=0,则m=1(舍)或-
| 1 |
| 2 |
∴切线l:y-1=
| 3 |
| 4 |
故切线方程为:3x-y-2=0或3x-4y+1=0.
点评:本题主要考查导数的几何意义、利用导数研究曲线上某点处的切线方程等基础知识,注意在某点处和过某点的切线,考查运算求解能力.属于中档题和易错题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列说法正确的是( )
| A、命题“?x0∈R,x02+x0+1<0”的否定是:“?x∈R,x2+x+1>0” |
| B、“x=-1”是“x2-5x-6=0”的必要不充分条件 |
| C、命题“若x2=1,则x=1”的否命题是:若x2=1,则x≠1 |
| D、命题“若x=y,则sin x=sin y”的逆否命题为真命题 |
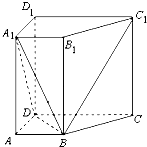 如图,已知在直四棱柱ABCD-A1B1C1D1(侧棱垂直底面的棱柱)中,AD⊥DC,AB∥DC,DC=DD1=2AD=2AB=2.
如图,已知在直四棱柱ABCD-A1B1C1D1(侧棱垂直底面的棱柱)中,AD⊥DC,AB∥DC,DC=DD1=2AD=2AB=2.