题目内容
设
=（m+1）i-3j，
=i+（m-1）j，（
+
）⊥（
-
），则m= ．
| a |
| b |
| a |
| b |
| a |
| b |
考点：数量积判断两个平面向量的垂直关系
专题：平面向量及应用
分析：由已知得
+
=（m+2，m-4），
-
=（m，-2-m），由（
+
）⊥（
-
），得（
+
）•（
-
）=m（m+2）+（m-4）（-2-m）=0，由此能求出m．
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
解答：
解：∵
=（m+1）i-3j，
=i+（m-1）j，
∴
+
=（m+2，m-4），
-
=（m，-2-m），
∵（
+
）⊥（
-
），
∴（
+
）•（
-
）=m（m+2）+（m-4）（-2-m）=0，
解得m=-2．
故答案为：-2．
| a |
| b |
∴
| a |
| b |
| a |
| b |
∵（
| a |
| b |
| a |
| b |
∴（
| a |
| b |
| a |
| b |
解得m=-2．
故答案为：-2．
点评：本题考查实数值的求法，是基础题，解题时要注意向量垂直的性质的合理运用．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
已知0＜a＜b，且a+b=1，则下列不等式①log2a＞-1；②log2a+log2b＞-2；③log2（b-a）＜0；④log2（
+
）＞1，其中一定成立的不等式的序号是（ ）
| b |
| a |
| a |
| b |
| A、①② | B、②③ | C、③④ | D、①④ |
曲线y=ex•lnx在（1，0）处在切线斜率为（ ）
| A、0 | ||
B、
| ||
| C、e | ||
| D、1 |
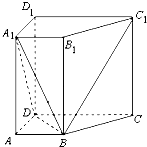如图，已知在直四棱柱ABCD-A1B1C1D1（侧棱垂直底面的棱柱）中，AD⊥DC，AB∥DC，DC=DD1=2AD=2AB=2．