题目内容
下述三个事件按顺序分别对应三个图象,正确的顺序是( )
①我离开家不久,发现自己把作业本忘在家里了,于是返回家里找到了作业本再上学;
②我骑着车一路匀速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
③我出发后,心情轻松,缓慢行进,后来为了赶时间开始加速.
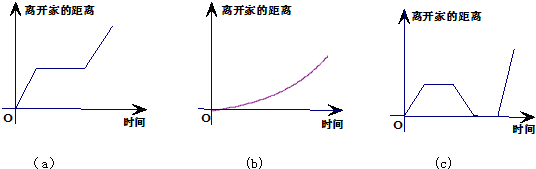
①我离开家不久,发现自己把作业本忘在家里了,于是返回家里找到了作业本再上学;
②我骑着车一路匀速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
③我出发后,心情轻松,缓慢行进,后来为了赶时间开始加速.

| A、abc | B、bac |
| C、cab | D、acb |
考点:函数的图象
专题:函数的性质及应用
分析:根据时间和离开家距离的关系进行判断.根据回家后,离家的距离又变为0,可判断(a)的图象开始后不久又回归为0;由途中遇到一次交通堵塞,可判断中间有一段函数值没有发生变化;由为了赶时间开始加速,可判断函数的图象上升速度越来越快.
解答:
解:(1)离家不久发现自己作业本忘记在家里,回到家里,这时离家的距离为0,故应先选图象(c);
(2)骑着车一路以常速行驶,此时为递增的直线,在途中遇到一次交通堵塞,则这段时间与家的距离必为一定值,故应选图象(a);
(3)我出发后,心情轻松,缓慢行进,后来为了赶时间开始加速,其距离与时间的关系为二次函数,故应选图象(b).
故选:C.
(2)骑着车一路以常速行驶,此时为递增的直线,在途中遇到一次交通堵塞,则这段时间与家的距离必为一定值,故应选图象(a);
(3)我出发后,心情轻松,缓慢行进,后来为了赶时间开始加速,其距离与时间的关系为二次函数,故应选图象(b).
故选:C.
点评:本题主要考查函数的图象的识别和判断,通过分析实际情况中离家距离随时间变化的趋势,找出关键的图象特征,对3个图象进行分析,即可得到答案.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
在等比数列{an}中,an>0,且a2a4+2a3a5+a4a6=25,那么a3+a5=( )
| A、5 | B、10 | C、15 | D、20 |
若关于x,y的不等式组
(k是常数)所表示的平面区域的边界是一个直角三角形,则k的值为( )
|
| A、0或1 | B、1或2 |
| C、0或2 | D、0或-1 |
下列函数中,以
为最小正周期的偶函数是( )
| π |
| 2 |
| A、y=sin2x+cos2x | ||
| B、y=sin2xcos2x | ||
C、y=cos(4x+
| ||
| D、y=sin22x-cos22x |
设复数z1=1+2i,z2=1+i,记复数z=
,则复数z在复平面内所对应的点位于( )
| z1 |
| z2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
设{an}是集合{2s+2t|0≤s<t,且s,t∈Z}中所有的数从小到大排成的数列,则a50的值是( )
| A、1024 | B、1032 |
| C、1040 | D、1048 |
 如图是某赛季甲、乙两名篮球运动员参加的每场比赛得分的茎叶图,由甲、乙两人这几场比赛得分的中位数之和是( )
如图是某赛季甲、乙两名篮球运动员参加的每场比赛得分的茎叶图,由甲、乙两人这几场比赛得分的中位数之和是( )| A、65 | B、64 | C、63 | D、62 |
已知函数y=x4-2x-2-1,则函数为( )
| A、奇函数 | B、偶函数 |
| C、非奇非偶 | D、既奇又偶 |