题目内容
已知数列:1,a+a2,a2+a3+a4,a3+a4+a5+a6,…,则数列的第k项为( )
| A、ak+ak+1+…+a2k |
| B、ak-1+ak+…+a2k-1 |
| C、ak-1+ak+…+a2k |
| D、ak-1+ak+…+a2k-2 |
考点:归纳推理
专题:推理和证明
分析:根据已知中数列的前4项,分析数列的项数及起始项的变化规律,进而可得答案.
解答:
解:由已知数列的前4项:
1,
a+a2,
a2+a3+a4,
a3+a4+a5+a6,
…,
归纳可得:该数列的第k项是一个:
以1为首项,以a为公比的等比数列第k项(ak-1)开始的连续k项和,
数列的第k项为:ak-1+ak+…+a2k-2
故选:D
1,
a+a2,
a2+a3+a4,
a3+a4+a5+a6,
…,
归纳可得:该数列的第k项是一个:
以1为首项,以a为公比的等比数列第k项(ak-1)开始的连续k项和,
数列的第k项为:ak-1+ak+…+a2k-2
故选:D
点评:本题主要考查了归纳推理,属于基础题.所谓归纳推理,就是从个别性知识推出一般性结论的推理.

练习册系列答案
相关题目
观察下列各式:则72=49,73=343,74=2401,…,则72014的末两位数字为( )
| A、01 | B、43 | C、07 | D、49 |
根据给出的数塔猜测123456×9+7=( )
1×9+2=11
12×9+3=111
123×9+4=1111
1234×9+5=11111
12345×9+6=111111
…
1×9+2=11
12×9+3=111
123×9+4=1111
1234×9+5=11111
12345×9+6=111111
…
| A、1111110 |
| B、1111111 |
| C、1111112 |
| D、1111113 |
2014°是第( )象限角.
| A、一 | B、二 | C、三 | D、四 |
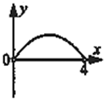
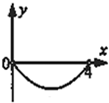
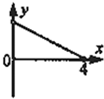
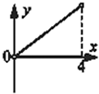
 如图,矩形纸片ABCD中,BC=4,AB=3,点P是BC边上的动点,现将△PCD沿PD翻折,得到△PFD;作∠BPF的角平分线交AB于点E.设BP=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
如图,矩形纸片ABCD中,BC=4,AB=3,点P是BC边上的动点,现将△PCD沿PD翻折,得到△PFD;作∠BPF的角平分线交AB于点E.设BP=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是( )