题目内容
△ABC中，角A，B，C所对的边分别是a，b，c，a=2csinA，则C为（ ）
| A、30° |
| B、60° |
| C、30°或150° |
| D、60°或120° |
考点：正弦定理
专题：解三角形
分析：已知等式利用正弦定理化简，根据sinA不为0，求出sinC的值，即可确定出C的度数．
解答：
解：已知等式a=2csinA，利用正弦定理化简得：sinA=2sinAsinC，
∵sinA≠0，
∴sinC=
，
则C=30°或150°．
故选：C．
∵sinA≠0，
∴sinC=
| 1 |
| 2 |
则C=30°或150°．
故选：C．
点评：此题考查了正弦定理，以及特殊角的三角函数值，熟练掌握正弦定理是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
在△ABC中，A，B，C是三角形的三内角，若sin（A-B）cosB+cos（A-B）sinB≥1，则该三角形是（ ）
| A、等腰三角形 | B、直角三角形 |
| C、正三角形 | D、不存在 |
下列推理正确的是（ ）
| A、如果不买彩票，那么就不能中奖，因为你买了彩票，所以你一定中奖 | ||||||||||||||
| B、∵a＞b，a＞c，∴a-b＞a-c | ||||||||||||||
C、若a∈R+，ab＜0，则
| ||||||||||||||
D、若a，b∈R+，则lga+lgb≥2
|
观察下列各式：则72=49，73=343，74=2401，…，则72014的末两位数字为（ ）
| A、01 | B、43 | C、07 | D、49 |
根据给出的数塔猜测123456×9+7=（ ）
1×9+2=11
12×9+3=111
123×9+4=1111
1234×9+5=11111
12345×9+6=111111
…
1×9+2=11
12×9+3=111
123×9+4=1111
1234×9+5=11111
12345×9+6=111111
…
| A、1111110 |
| B、1111111 |
| C、1111112 |
| D、1111113 |
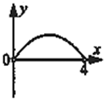
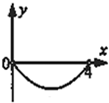
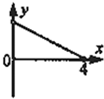
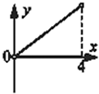
如图，矩形纸片ABCD中，BC=4，AB=3，点P是BC边上的动点，现将△PCD沿PD翻折，得到△PFD；作∠BPF的角平分线交AB于点E．设BP=x，BE=y，则下列图象中，能表示y与x的函数关系的图象大致是（ ）
