题目内容
已知四面体A-BCD的棱长都相等,Q是AD的中点,求CQ与平面DBC所成的角的正弦值.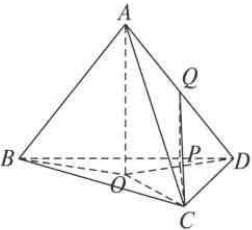

考点:直线与平面所成的角
专题:空间位置关系与距离
分析:作DE⊥BC,交BC于E,作AO⊥平在BDC,交DE于O,作QP⊥平面BDC,交DE于P,连结QC,CP,则∠PCQ是CQ与平面DBC所成角,由此能求出CQ与平面DBC所成角的正弦值.
解答:
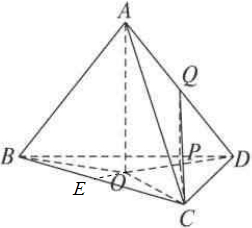 解:作DE⊥BC,交BC于E,作AO⊥平在BDC,交DE于O,
解:作DE⊥BC,交BC于E,作AO⊥平在BDC,交DE于O,
作PQ⊥平面BDC,交DE于P,连结QC,CP,
则∠PCQ是CQ与平面DBC所成角,
设正四面体ABCD的棱长为2,
则DE=QC=DE=
=
,
DO=
DE=
,DP=
,
AO=
=
,PQ=
AO=
,
∴sin∠PCQ=
=
=
.
∴CQ与平面DBC所成角的正弦值为
.
 解:作DE⊥BC,交BC于E,作AO⊥平在BDC,交DE于O,
解:作DE⊥BC,交BC于E,作AO⊥平在BDC,交DE于O,作PQ⊥平面BDC,交DE于P,连结QC,CP,
则∠PCQ是CQ与平面DBC所成角,
设正四面体ABCD的棱长为2,
则DE=QC=DE=
| 22-12 |
| 3 |
DO=
| 2 |
| 3 |
2
| ||
| 3 |
| ||
| 3 |
AO=
4-
|
2
| ||
| 3 |
| 1 |
| 2 |
| ||
| 3 |
∴sin∠PCQ=
| PQ |
| QC |
| ||||
|
| ||
| 3 |
∴CQ与平面DBC所成角的正弦值为
| ||
| 3 |
点评:本题考查直线与平面所成角的正弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
已知定义在[1-2a,2-a]上的偶函数f(x),当x≥0时,f(x)=x+ex,若f(t)<f(2t-1).则t的取值范围是( )
| A、[-1,1] | ||
| B、[0,1] | ||
C、[
| ||
D、[0,
|
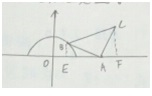 已知B是x2+y2=1(y∈[0,1])上一动点,A(2,0)△ABC是以A为直角顶点的等腰三角形,且A,B,C按顺时针方向排列,则动点C的轨迹方程是
已知B是x2+y2=1(y∈[0,1])上一动点,A(2,0)△ABC是以A为直角顶点的等腰三角形,且A,B,C按顺时针方向排列,则动点C的轨迹方程是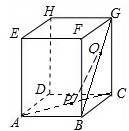 如图,正方体ABCD-EFGH的棱长为a,点P在AC上,点Q在BG上,AP=BQ=a,求证:PQ⊥AD.
如图,正方体ABCD-EFGH的棱长为a,点P在AC上,点Q在BG上,AP=BQ=a,求证:PQ⊥AD.