题目内容
已知函数y=f(x)满足:①y=f(x+1)是偶函数;②在区间[1,+∞)上是增函数.若x1<x2<0且x1+x2<-2,则f(-x1)与f(-x2)的大小关系是( )
| A、f(-x1)>f(-x2) |
| B、f(-x1)<f(-x2) |
| C、f(-x1)=f(-x2) |
| D、无法确定 |
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:根据条件得到函数x=1对称,利用函数单调性和对称性之间的关系,即可得到结论.
解答:
解:∵y=f(x+1)是偶函数,∴f(-x+1)=f(x+1),
则函数f(x)关于x=1对称,
若x1<x2<0且x1+x2<-2,
则2+x1<-x2<0,
∵在区间[1,+∞)上是增函数,
∴在区间(-∞,1上是减函数,
则f(2+x1)>f(-x2),
即f(-x1)>f(-x2),
故选:A
则函数f(x)关于x=1对称,
若x1<x2<0且x1+x2<-2,
则2+x1<-x2<0,
∵在区间[1,+∞)上是增函数,
∴在区间(-∞,1上是减函数,
则f(2+x1)>f(-x2),
即f(-x1)>f(-x2),
故选:A
点评:本题主要考查函数值的大小比较,根据函数的对称性和单调性之间的关系是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知θ为第一象限角,设向量
=(sinθ,
),向量
=(cosθ,3),且
∥
,则θ一定为( )
| a |
| 3 |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列说法正确的是( )
| A、三点确定一个平面 |
| B、四边形一定是平面图形 |
| C、梯形一定是平面图形 |
| D、平面和平面可能有不同在一条直线上的三个交点 |
设集合S={x||x|<5},T={x|(x+7)(3-x)>0},则S∩T=( )
| A、{x|-7<x<-5} |
| B、{x|3<x<5} |
| C、{x|-5<x<3} |
| D、{x|-7<x<5} |
函数y=ax-2(a>0且a≠1)过定点( )
| A、(1,2) |
| B、(2,1) |
| C、(2,0) |
| D、(0,2) |
已知函数f(x)=log
cos
,x∈(0,1),函数g(x)=asin(
x)-2a+2(a>0),x∈(0,1).若存在x1,x2∈(0,1),使得f(x1)=g(x2)成立,则实数a的取值范围是( )
| 1 |
| 2 |
| πx |
| 3 |
| π |
| 6 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
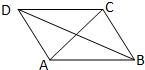 如图平行四边形ABCD中,
如图平行四边形ABCD中,| AC |
| BD |
| AD |
| AC |
| A、1 | B、2 | C、3 | D、4 |