题目内容
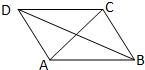如图平行四边形ABCD中，| AC |
| BD |
| AD |
| AC |
| A、1 | B、2 | C、3 | D、4 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由条件根据两个向量的加减法的法则，以及其几何意义，可得
+
=
=（1，2），
-
=
=（-3，2），求得
和
的坐标，可得
•
的值．
| AD |
| AB |
| AC |
| AD |
| AB |
| BD |
| AD |
| AB |
| AD |
| AC |
解答：
解：在平行四边形ABCD中，由于
+
=
=（1，2），
-
=
=（-3，2），
∴
=（-1，2），
=（-2，0），∴
•
=（-1，2）•（1，2）=-1+4=3，
故选：C．
| AD |
| AB |
| AC |
| AD |
| AB |
| BD |
∴
| AD |
| AB |
| AD |
| AC |
故选：C．
点评：本题主要考查两个向量的加减法的法则，以及其几何意义，两个向量坐标形式的运算，属于基础题．
练习册系列答案
相关题目
已知函数y=f（x）满足：①y=f（x+1）是偶函数；②在区间[1，+∞）上是增函数．若x1＜x2＜0且x1+x2＜-2，则f（-x1）与f（-x2）的大小关系是（ ）
| A、f（-x1）＞f（-x2） |
| B、f（-x1）＜f（-x2） |
| C、f（-x1）=f（-x2） |
| D、无法确定 |
已知函数f（x）=
在（-
，+∞）上单调递减，那么实数a的取值范围是（ ）
|
| π |
| 2 |
A、（
| ||||
B、（0，
| ||||
C、[
| ||||
D、[
|
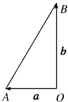
设
表示向西走10km，
表示向北走10
km，则
-
表示（ ）
| a |
| b |
| 3 |
| a |
| b |
| A、南偏西30°走20 km |
| B、北偏西30°走20 km |
| C、南偏东30°走20 km |
| D、北偏东30°走20 km |
一个平面封闭区域内任意两点距离的最大值称为该区域的“直径”，封闭区域边界曲线的长度与区域直径之比称为区域的“周率”，下面四个平面区域（阴影部分）的周率从左到右依次记为τ1，τ2，τ3，τ4，则下列关系中正确的为（ ）
| A、τ1＞τ4＞τ3 |
| B、τ3＞τ1＞τ2 |
| C、τ4＞τ2＞τ3 |
| D、τ3＞τ4＞τ1 |
若集合A={x∈R|lgx2＞0}，集合B={x∈R|1≤2x+3＜7}，则（ ）
| A、∁UB⊆A |
| B、B⊆A |
| C、A⊆∁UB |
| D、A⊆B |
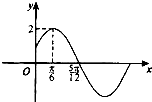已知函数f（x）=2sin（ωx+φ）（ω＞0，|φ|＜| π |
| 2 |
A、f（x）=2sin（
| ||||
B、f（x）=2sin（
| ||||
C、f（x）=2sin（2x-
| ||||
D、f（x）=2sin（2x+
|
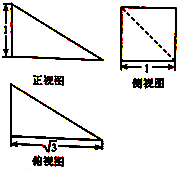
某几何体的三视图如图所示，则该几何体的外接球的球面面积为（ ）
| A、5π | B、12π |
| C、20π | D、8π |