题目内容
已知函数f(x)=log
cos
,x∈(0,1),函数g(x)=asin(
x)-2a+2(a>0),x∈(0,1).若存在x1,x2∈(0,1),使得f(x1)=g(x2)成立,则实数a的取值范围是( )
| 1 |
| 2 |
| πx |
| 3 |
| π |
| 6 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
考点:三角函数的最值
专题:三角函数的求值
分析:先由条件求得f(x)的值域,函数g(x)的值域,再根据这两个函数的值域的交集非空,求得a的范围.
解答:
解:由于x∈(0,1),可得f(x)的值域为(0,1),
函数g(x)=asin(
x)-2a+2(a>0)的值域为(2-2a,2-
),
f(x)=log
cos
,x∈(0,1)的值域为(0,1),
若存在x1,x2∈(0,1),使得f(x1)=g(x2)成立,
则(0,1)∩(2-2a,2-
)≠∅,
若(0,1)∩(2-2a,2-
)=∅,则有2-2a≥1,或 2-
≤0.
解得 a≤
,或a≥
,故要求的实数a的取值范围是(
,
),
故选:C.
函数g(x)=asin(
| π |
| 6 |
| 3a |
| 2 |
f(x)=log
| 1 |
| 2 |
| πx |
| 3 |
若存在x1,x2∈(0,1),使得f(x1)=g(x2)成立,
则(0,1)∩(2-2a,2-
| 3a |
| 2 |
若(0,1)∩(2-2a,2-
| 3a |
| 2 |
| 3a |
| 2 |
解得 a≤
| 1 |
| 2 |
| 4 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
故选:C.
点评:本题主要考查复合三角函数的单调性,正弦函数、余弦函数的值域,体现了转化的数学思想,属于中档题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
已知函数y=f(x)满足:①y=f(x+1)是偶函数;②在区间[1,+∞)上是增函数.若x1<x2<0且x1+x2<-2,则f(-x1)与f(-x2)的大小关系是( )
| A、f(-x1)>f(-x2) |
| B、f(-x1)<f(-x2) |
| C、f(-x1)=f(-x2) |
| D、无法确定 |
已知函数f(x)=-ex-1,g(x)=ln(x2+x+
).若有f(a)=g(b),则b的取值范围为( )
| 1 |
| e |
| A、[-1,0] | ||
| B、(-1,0) | ||
C、(
| ||
D、[
|
已知函数f(x)=
在(-
,+∞)上单调递减,那么实数a的取值范围是( )
|
| π |
| 2 |
A、(
| ||||
B、(0,
| ||||
C、[
| ||||
D、[
|
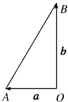
设
表示向西走10km,
表示向北走10
km,则
-
表示( )
| a |
| b |
| 3 |
| a |
| b |

| A、南偏西30°走20 km |
| B、北偏西30°走20 km |
| C、南偏东30°走20 km |
| D、北偏东30°走20 km |
某几何体的三视图如图所示,则该几何体的外接球的球面面积为( )
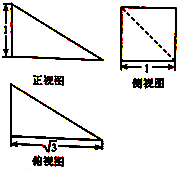

| A、5π | B、12π |
| C、20π | D、8π |