题目内容
函数y=ax-2（a＞0且a≠1）过定点（ ）
| A、（1，2） |
| B、（2，1） |
| C、（2，0） |
| D、（0，2） |
考点：指数函数的图像与性质
专题：函数的性质及应用
分析：利用指数函数的性质即可求得y=ax-2过定点．
解答：
解：∵y=ax-2，
∴当x-2=0时，即x=2时，y=1．
∴y=ax-2过定点（2，1）．
故选：B．
∴当x-2=0时，即x=2时，y=1．
∴y=ax-2过定点（2，1）．
故选：B．
点评：本题考查指数函数的性质，考查曲线过定点问题，令幂指数为0是解决问题的关键，属于基础题．
练习册系列答案
提分百分百检测卷系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
下列命题中，正确的是（ ）
| A、a=（-2，5）与b=（4，-10）方向相同 |
| B、a=（4，10）与b=（-2，-5）方向相反 |
| C、a=（-3，1）与b=（-2，-5）方向相反 |
| D、a=（2，4）与b=（-3，1）的夹角为锐角 |
已知函数y=f（x）满足：①y=f（x+1）是偶函数；②在区间[1，+∞）上是增函数．若x1＜x2＜0且x1+x2＜-2，则f（-x1）与f（-x2）的大小关系是（ ）
| A、f（-x1）＞f（-x2） |
| B、f（-x1）＜f（-x2） |
| C、f（-x1）=f（-x2） |
| D、无法确定 |
把函数y=sin（2x+
）的图象向右平移
个单位，再把所得图象上各点的横坐标缩短到原来的
，则所得图象的函数解析式是（ ）
| π |
| 4 |
| π |
| 8 |
| 1 |
| 2 |
A、y=sin（4x+
| ||
B、y=sin（4x+
| ||
| C、y=sin4x | ||
| D、y=sinx |
已知函数f（x）=
在（-
，+∞）上单调递减，那么实数a的取值范围是（ ）
|
| π |
| 2 |
A、（
| ||||
B、（0，
| ||||
C、[
| ||||
D、[
|
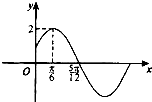已知函数f（x）=2sin（ωx+φ）（ω＞0，|φ|＜| π |
| 2 |
A、f（x）=2sin（
| ||||
B、f（x）=2sin（
| ||||
C、f（x）=2sin（2x-
| ||||
D、f（x）=2sin（2x+
|