题目内容
已知函数f(x)=ln|x|,(x≠0),函数g(x)=
+af′(x),a∈R.
(1)求函数y=g(x)的表达式和单调区间;
(2)若a>0,函数y=g(x)在(0,+∞)上的最小值是2,求a的值.
| 1 |
| f′(x) |
(1)求函数y=g(x)的表达式和单调区间;
(2)若a>0,函数y=g(x)在(0,+∞)上的最小值是2,求a的值.
考点:利用导数研究函数的单调性,函数解析式的求解及常用方法,函数单调性的判断与证明
专题:导数的综合应用
分析:(1)求函数的导数,根据函数单调性和导数之间的关系即可,求函数y=g(x)的表达式和单调区间;
(2)根据基本不等式求出函数的最小值,建立方程关系即可得到结论.
(2)根据基本不等式求出函数的最小值,建立方程关系即可得到结论.
解答:
(Ⅰ)∵f(x)=ln|x|,
∴当x>0时,f(x)=lnx; 当x<0时,f(x)=ln(-x),
∴当x>0时,f′(x)=
; 当x<0时,f′(x)=
•(-1)=
.
∴当x≠0时,函数g(x)=
+af′(x)=x+
;
则g′(x)=1-
=
,
若a≤0,则g′(x)≥0;此时函数单调递增,即函数的增区间为(0,+∞),(-∞,0).
若a>0,由g′(x)≥0,解得x≥
或x≤-
,即函数的增区间为(
,+∞),(-∞,-
).
由g′(x)≤0,解得-
≤x<0或0<x≤
,即函数的减区间为[-
,0),(0,
].
(Ⅱ)∵由(1)知当x>0时,g(x)=x+
,
∴当a>0,x>0时,g(x)=x+
≥2
,当且仅当x=
时取等号.
∴函数y=g(x)在(0,+∞)上的最小值是2
=2,
即
=1,得a=1.
∴当x>0时,f(x)=lnx; 当x<0时,f(x)=ln(-x),
∴当x>0时,f′(x)=
| 1 |
| x |
| 1 |
| -x |
| 1 |
| x |
∴当x≠0时,函数g(x)=
| 1 |
| f′(x) |
| a |
| x |
则g′(x)=1-
| a |
| x2 |
| x2-a |
| x2 |
若a≤0,则g′(x)≥0;此时函数单调递增,即函数的增区间为(0,+∞),(-∞,0).
若a>0,由g′(x)≥0,解得x≥
| a |
| a |
| a |
| a |
由g′(x)≤0,解得-
| a |
| a |
| a |
| a |
(Ⅱ)∵由(1)知当x>0时,g(x)=x+
| a |
| x |
∴当a>0,x>0时,g(x)=x+
| a |
| x |
| a |
| a |
∴函数y=g(x)在(0,+∞)上的最小值是2
| a |
即
| a |
点评:本题主要考查函数单调区间的求解,利用函数单调性和导数之间的关系是解决本题的关键.

练习册系列答案
相关题目
 已知如图,△ABC是边长为1的正三角形,PA⊥平面ABC,且
已知如图,△ABC是边长为1的正三角形,PA⊥平面ABC,且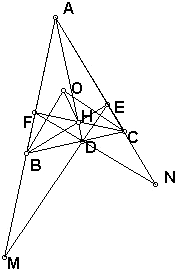 如图,△ABC中,O为外心,三条高AD、BE、CF交于点H,直线ED和AB交于点M,FD和AC交于点N.求证:OB⊥DF.
如图,△ABC中,O为外心,三条高AD、BE、CF交于点H,直线ED和AB交于点M,FD和AC交于点N.求证:OB⊥DF.