题目内容
已知椭圆C的方程为
+
=1.
(Ⅰ)求椭圆C的长轴长及离心率;
(Ⅱ)已知直线l过(1,0),与椭圆C交于A,B两点,M为椭圆C的左顶点.是否存在直线l使得∠AMB=60°?如果有,求出直线l的方程;如果没有,请说明理由.
| x2 |
| 4 |
| y2 |
| 16 |
(Ⅰ)求椭圆C的长轴长及离心率;
(Ⅱ)已知直线l过(1,0),与椭圆C交于A,B两点,M为椭圆C的左顶点.是否存在直线l使得∠AMB=60°?如果有,求出直线l的方程;如果没有,请说明理由.
考点:直线与圆锥曲线的关系,椭圆的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)由椭圆C的方程为
+
=1,确定椭圆的几何量,即可求椭圆C的长轴长及离心率;
(Ⅱ)分类讨论,设直线l的方程,与椭圆方程联立,利用韦达定理及向量的数量积,可得
•
<0恒成立,∠AMB为钝角,即可得到结论.
| x2 |
| 4 |
| y2 |
| 16 |
(Ⅱ)分类讨论,设直线l的方程,与椭圆方程联立,利用韦达定理及向量的数量积,可得
| MA |
| MB |
解答:
解:(Ⅰ)由方程
2+
=1可知a=4,b=2
所以长轴长为8,且c2=a2-b2=12
所以离心率
.
(Ⅱ)(1)当直线l的斜率不存在时,A(1,2
),B(1,-2
)
•
=-3
(2)当直线l的斜率存在时,设直线l的方程为y=k(x-1),
设A(x1,y1),B(x2,y2),
由
消去y得:(4+k2)x2-2k2x+k2-16=0.
则
,
•
=(x1+2)(x2+2)+y1y2=(x1+2)(x2+2)+k(x1-1)k(x2-1)
=(k2+1)x1x2+(2-k2)(x1+x2)+4+k2=
<0
综上,
•
<0恒成立,∠AMB为钝角
所以,不存在直线l使得∠AMB=60°
| x |
| 4 |
| y2 |
| 16 |
所以长轴长为8,且c2=a2-b2=12
所以离心率
| ||
| 2 |
(Ⅱ)(1)当直线l的斜率不存在时,A(1,2
| 3 |
| 3 |
| MA |
| MB |
(2)当直线l的斜率存在时,设直线l的方程为y=k(x-1),
设A(x1,y1),B(x2,y2),
由
|
则
|
| MA |
| MB |
=(k2+1)x1x2+(2-k2)(x1+x2)+4+k2=
| -3k2 |
| 4+k2 |
综上,
| MA |
| MB |
所以,不存在直线l使得∠AMB=60°
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查向量知识,解题的关键是直线与椭圆联立,利用韦达定理进行求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
i是虚数单位,若集合S={-2,0,1},则( )
| A、i2015∈S | ||
| B、-2i2014∈S | ||
| C、i2013∈S | ||
D、i(i-
|
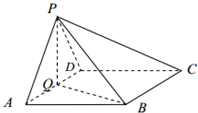 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.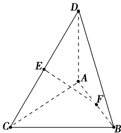 已知DA⊥平面ABC,AC⊥CB,AC=CB=AD=2,E是DC的中点,F是AB的中点.
已知DA⊥平面ABC,AC⊥CB,AC=CB=AD=2,E是DC的中点,F是AB的中点.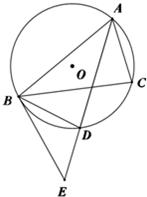 如图,A,B,C是圆O上三个点,AD是∠BAC的平分线,交圆O于D,过B做直线BE交AD延长线于E,使BD平分∠EBC.
如图,A,B,C是圆O上三个点,AD是∠BAC的平分线,交圆O于D,过B做直线BE交AD延长线于E,使BD平分∠EBC.