题目内容
在锐角△ABC中，a，b，c分别为角A，B，C所对的边，且
b=2csinB．
（1）求角C的大小．
（2）若c=4，且△ABC的面积为4
，求△ABC的周长．
| 3 |
（1）求角C的大小．
（2）若c=4，且△ABC的面积为4
| 3 |
考点：余弦定理,正弦定理
专题：解三角形
分析：（1）利用正弦定理求出角C的三角函数值，然后求出C的大小．
（2）利用△ABC的面积为4
，以及余弦定理列出关系式求出a+b，然后求△ABC的周长．
（2）利用△ABC的面积为4
| 3 |
解答：
解：（1）在锐角△ABC中，a，b，c分别为角A，B，C所对的边，且
b=2csinB．
由正弦定理可得：
sinB=2sinCsinB，
∴sinC=
，角C的大小为：60°．
（2）若c=4，且△ABC的面积为4
，
∴
absinC=4
，即ab=16，
由余弦定理可得：16=a2+b2-2abcos60°，即a2+b2=32．
∴（a+b）2=64，∴a+b=8，
∴△ABC的周长a+b+c=12．
| 3 |
由正弦定理可得：
| 3 |
∴sinC=
| ||
| 2 |
（2）若c=4，且△ABC的面积为4
| 3 |
∴
| 1 |
| 2 |
| 3 |
由余弦定理可得：16=a2+b2-2abcos60°，即a2+b2=32．
∴（a+b）2=64，∴a+b=8，
∴△ABC的周长a+b+c=12．
点评：本题考查余弦定理以及正弦定理的应用，基本知识的考查．
练习册系列答案
字词句篇与同步作文达标系列答案
走进文言文系列答案
相关题目
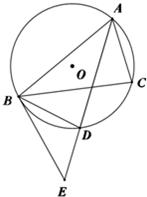如图，A，B，C是圆O上三个点，AD是∠BAC的平分线，交圆O于D，过B做直线BE交AD延长线于E，使BD平分∠EBC．