题目内容
设数列{an}的前n项和为Sn,a1=10,an+1=9Sn+10,设Tn是数列{
}的前n项和,求使Tn>
(m2-5m)对所有的n∈N成立的最大正整数m的值集合.
| 3 |
| (lgan)(lgan+1) |
| 1 |
| 4 |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)利用an与sn的关系得,an+1=9Sn+10,an=9Sn-1+10,两式作差即可证得数列{an}是以10为首项,10为公比的等比数列,进而求得an=a1qn-1=10n,lgan=n,
(2)利用裂项相消法求得Tn,Tn≥
,依题意有
>
(m2-5m),解不等式即可得出结论.
(2)利用裂项相消法求得Tn,Tn≥
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 4 |
解答:
解:依题意,
当n=1时,a2=9S1+10=9×10+10=100;
当n≥2时,由an+1=9Sn+10,an=9Sn-1+10,
可得an+1-an=9an,即an+1=10an,此式对于n=1时也成立.
∴数列{an}是以10为首项,10为公比的等比数列,
∴an=a1qn-1=10n,∴lgan=n,
∴
=
=
-
,
∴Tn=3(1-
+
-
+…+
-
)=3(1-
)=3-
,
∴Tn≥
,
依题意有
>
(m2-5m),解得-1<m<6,
故所求最大正整数m的值为5.
当n=1时,a2=9S1+10=9×10+10=100;
当n≥2时,由an+1=9Sn+10,an=9Sn-1+10,
可得an+1-an=9an,即an+1=10an,此式对于n=1时也成立.
∴数列{an}是以10为首项,10为公比的等比数列,
∴an=a1qn-1=10n,∴lgan=n,
∴
| 1 |
| (lgan)(lgan+1) |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴Tn=3(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
| 3 |
| n+1 |
∴Tn≥
| 3 |
| 2 |
依题意有
| 3 |
| 2 |
| 1 |
| 4 |
故所求最大正整数m的值为5.
点评:本题主要考查了等差数列和等比数列的性质.考查了学生对数列基础知识的综合把握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
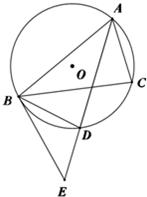 如图,A,B,C是圆O上三个点,AD是∠BAC的平分线,交圆O于D,过B做直线BE交AD延长线于E,使BD平分∠EBC.
如图,A,B,C是圆O上三个点,AD是∠BAC的平分线,交圆O于D,过B做直线BE交AD延长线于E,使BD平分∠EBC.