题目内容
已知函数f(x)=(
)x,函数g(x)=log
x
(1)若g(mx2+2x+m)的定义域为R,求实数m的取值范围
(2)当x∈[-1,1]时,求函数y=[f(x)]2-2af(x)+3的最小值h(a)
| 1 |
| 3 |
| 1 |
| 3 |
(1)若g(mx2+2x+m)的定义域为R,求实数m的取值范围
(2)当x∈[-1,1]时,求函数y=[f(x)]2-2af(x)+3的最小值h(a)
考点:函数的最值及其几何意义
专题:函数的性质及应用
分析:(1)若g(mx2+2x+m)的定义域为R,结合对数函数的性质建立不等式恒成立,即可求实数m的取值范围.
(2)利用换元法设t=(
)x,将函数转化为一元二次函数,利用一元二次函数的性质即可求出函数的最小值.
(2)利用换元法设t=(
| 1 |
| 3 |
解答:
解:(1)∵g(mx2+2x+m)=log
(mx2+2x+m)的定义域为R,
则等价为不等式mx2+2x+m>0的解集为R,
当m=0是,不等式等价为x>0,此时不满足条件.
当m≠0,
则等价为
,
即
,
解得m>1.
(2)令t=(
)x,
∵x∈[-1,1],
∴t∈[
,3],
则y=[f(x)]2-2af(x)+3等价为y=m(t)=t2-2at+3,
对称轴为t=a,
当a<
时,函数的最小值为h(a)=m(
)=
;
当
≤a≤3时,函数的最小值为h(a)=m(a)=3-a2;
当a>3时,函数的最小值为h(a)=m(3)=12-6a;
综上所述,h(a)=
.
| 1 |
| 3 |
则等价为不等式mx2+2x+m>0的解集为R,
当m=0是,不等式等价为x>0,此时不满足条件.
当m≠0,
则等价为
|
即
|
解得m>1.
(2)令t=(
| 1 |
| 3 |
∵x∈[-1,1],
∴t∈[
| 1 |
| 3 |
则y=[f(x)]2-2af(x)+3等价为y=m(t)=t2-2at+3,
对称轴为t=a,
当a<
| 1 |
| 3 |
| 1 |
| 3 |
| 28-6a |
| 9 |
当
| 1 |
| 3 |
当a>3时,函数的最小值为h(a)=m(3)=12-6a;
综上所述,h(a)=
|
点评:本题主要考查函数最值的应用,利用对数函数的性质,利用换元法结合一元二次函数的性质是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列各角中与240°角终边相同的角为( )
A、
| ||
B、-
| ||
C、-
| ||
D、
|
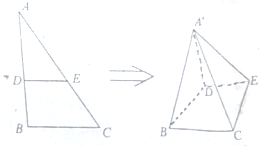 如图,在直角△ABC中,B=90°,BC=1,AB=
如图,在直角△ABC中,B=90°,BC=1,AB=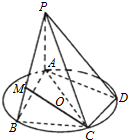 如图AC是圆O的直径,B、D是圆O上两点,AC=2BC=2CD=2,PA⊥圆O所在的平面,
如图AC是圆O的直径,B、D是圆O上两点,AC=2BC=2CD=2,PA⊥圆O所在的平面,