题目内容
已知数列{bn}的通项公式bn=log2
,Tn为bn的前n项和,求证:2Tn>log2(2n+1),n∈N*.
| 2n |
| 2n-1 |
考点:数列的求和
专题:计算题,综合题
分析:由不等式(2n)2>(2n+1)(2n-1),得(
)2>
,两边取对数后利用对数的运算性质展开,然后裂项求和证得答案.
| 2n |
| 2n-1 |
| 2n+1 |
| 2n-1 |
解答:
解:∵(2n)2>(2n+1)(2n-1),∴(
)2>
,
两边取对数得2log2
>log2
,
即2bn>log2(2n+1)-log2(2n-1),
∴2Tn>(log23-log21)+(log25-log23)+…+[log2(2n+1)-log2(2n-1)]=log2(2n+1).
| 2n |
| 2n-1 |
| 2n+1 |
| 2n-1 |
两边取对数得2log2
| 2n |
| 2n-1 |
| 2n+1 |
| 2n-1 |
即2bn>log2(2n+1)-log2(2n-1),
∴2Tn>(log23-log21)+(log25-log23)+…+[log2(2n+1)-log2(2n-1)]=log2(2n+1).
点评:本题考查了裂项相消法求数列的和,考查了对数式的运算性质,考查了放缩法证明数列不等式,是中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
在正四棱锥P-ABCD中,PA=
AB,M是BC的中点,G是△PAD的重心,则在平面PAD中经过点G且与直线PM垂直的直线条数有( )
| ||
| 2 |
| A、0条 | B、1条 | C、3条 | D、无数条 |
数列an=
的前5项之和是( )
| 1+(-1)n |
| 2 |
| A、0 | B、2 | C、4 | D、6 |
已知角α终边上一点的坐标是(sin
,cos
),则角α的值是( )
| π |
| 5 |
| π |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、(-1)k
|
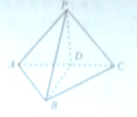 如图所示,在四面体P-ABC中,∠ABC=90°,PA=PB=PC,D是AC的中点,求证:PD垂直于△ABC所在的平面.
如图所示,在四面体P-ABC中,∠ABC=90°,PA=PB=PC,D是AC的中点,求证:PD垂直于△ABC所在的平面.