题目内容
1.设P是双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{2}$=1上的动点,若P到两条渐近线的距离分别为d1、d2,则d1•d2=( )| A. | 3$\sqrt{2}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | 2$\sqrt{3}$ |
分析 求出渐近线方程,设双曲线C上的点P(x,y),求出点P到两条渐近线的距离,结合P在双曲线C上,即可求d1•d2的值.
解答 解:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{2}$=1,可得x2-2y2=4,
由条件可知:两条渐近线分别为x±$\sqrt{2}$y=0,
设双曲线C上的点P(x,y),
则点P到两条渐近线的距离分别为d1=$\frac{|x+\sqrt{2}y|}{\sqrt{3}}$,d2=$\frac{|x-\sqrt{2}y|}{\sqrt{3}}$,
所以d1•d2=$\frac{|{x}^{2}-2{y}^{2}|}{3}$=$\frac{4}{3}$.
故选:B.
点评 本题考查双曲线的标准方程,考查双曲线的几何性质,求出点P到两条渐近线的距离是关键,属于中档题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
相关题目
11.设f(x)是周期为4的偶函数,当x∈[0,2]时,f(x)=$\sqrt{3}$tan$\frac{πx}{6}$,若在区间(-2,6)内关于x的方程f(x)-ax-a=0恰有3个不同实数根,则正数a的取值范围是( )
| A. | ($\frac{3}{7}$,1) | B. | ($\frac{3}{4}$,1) | C. | (0,$\frac{3}{7}$) | D. | (0,$\frac{3}{4}$) |
12.某校高一(1)、(2)两个班联合开展“诗词大会进校园,国学经典润心田”古诗词竞赛主题班会活动,主持人从这两个班分别随机选出20名同学进行当场测试,他们的测试成绩按[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)分组,分组用频率分布直方图与茎叶统计如下(单位:分)
(1)班20名同学成绩频率分布直方图
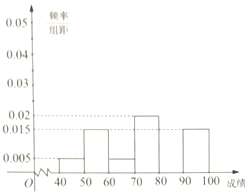
(2)班20名同学成绩茎叶图
(Ⅰ)分別计算两个班这20名同学的测试成绩在[80,90)的频率,并补全频率分布直方图;
(Ⅱ)从(2)班参加测试的不低于80分的同学中随机选取两人,求这两人中至少有1人的成绩在90分以上的概率;
(III )运用所学统计知识分析比较两个班学生的古诗词水平.
(1)班20名同学成绩频率分布直方图

(2)班20名同学成绩茎叶图
| 4 | 5 |
| 5 | 2 |
| 6 | 4 5 6 8 |
| 7 | 0 5 5 8 8 8 8 9 |
| 8 | 005 5 |
| 9 | 45 |
(Ⅱ)从(2)班参加测试的不低于80分的同学中随机选取两人,求这两人中至少有1人的成绩在90分以上的概率;
(III )运用所学统计知识分析比较两个班学生的古诗词水平.