题目内容
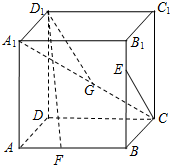 已知正方体ABCD-A1B1C1D1,点E,F,G分别是线段B1B,AB和A1C上的动点,观察直线CE与D1F,CE与D1G.给出下列结论:
已知正方体ABCD-A1B1C1D1,点E,F,G分别是线段B1B,AB和A1C上的动点,观察直线CE与D1F,CE与D1G.给出下列结论:①对于任意给定的点E,存在点F,使得D1F⊥CE;
②对于任意给定的点F,存在点E,使得CE⊥D1F;
③对于任意给定的点E,存在点G,使得D1G⊥CE;
④对于任意给定的点G,存在点E,使得CE⊥D1G.
其中正确结论的序号是( )
| A、①③ | B、①④ | C、②③ | D、②④ |
考点:空间中直线与直线之间的位置关系
专题:综合题,空间位置关系与距离
分析:根据直线与直线、直线与平面的位置关系,利用排除法能得出结论.
解答:
解:①只有D1F⊥平面BCC1B1,即D1F⊥平面ADD1A1时,
才能满足对于任意给定的点E,存在点F,使得D1F⊥CE,
∵过D1点于平面DD1A1A垂直的直线只有一条D1C1,
而D1C1∥AB,
∴①错误;
②当点E与B1重合时,
CE⊥AB,且CE⊥AD1,
∴CE⊥平面ABD1,
∵对于任意给定的点F,都有D1F?平面ABD1,
∴对于任意给定的点F,存在点E,使得CE⊥D1F,
∴②正确;
③只有CE⊥D1G在平面BCC1B1中的射影时,D1G⊥CE,
∴③正确;④只有CE⊥平面A1CD1时,④才正确,
∵过C点的平面A1CD1的垂线与BB1无交点,
∴④错误.
故选:C.
才能满足对于任意给定的点E,存在点F,使得D1F⊥CE,
∵过D1点于平面DD1A1A垂直的直线只有一条D1C1,
而D1C1∥AB,
∴①错误;
②当点E与B1重合时,
CE⊥AB,且CE⊥AD1,
∴CE⊥平面ABD1,
∵对于任意给定的点F,都有D1F?平面ABD1,
∴对于任意给定的点F,存在点E,使得CE⊥D1F,
∴②正确;
③只有CE⊥D1G在平面BCC1B1中的射影时,D1G⊥CE,
∴③正确;④只有CE⊥平面A1CD1时,④才正确,
∵过C点的平面A1CD1的垂线与BB1无交点,
∴④错误.
故选:C.
点评:本题考查直线与直线、直线与平面的位置关系的判断,是中档题,解题时要注意空间思维能力的培养.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
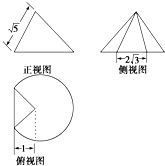 一个圆锥被过其顶点的一个平面截去了较少的一部分几何体,余下的几何体的三视图如图,则余下部分的几何体的体积为( )
一个圆锥被过其顶点的一个平面截去了较少的一部分几何体,余下的几何体的三视图如图,则余下部分的几何体的体积为( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
如图所示是函数y=f(x)的图象,则函数y=f(x)的导函数图象是( )


A、 |
B、 |
C、 |
D、 |
设△ABC的内角A、B、C的对边分别为a、b、c,若
=
=
,则△ABC是( )
| a | ||
cos
|
| b | ||
cos
|
| c | ||
cos
|
| A、直角三角形 |
| B、钝角三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
如图,A1B1C1-ABC是三棱柱,下列直线中与AA1成异面直线的是( )


| A、BB1 |
| B、CC1 |
| C、B1C1 |
| D、AB |
已知函数f(x)=
x3+ax2-4在区间(0,2)上是减函数,则a的范围是( )
| 1 |
| 3 |
| A、(-∞,3] |
| B、[-1,+∞) |
| C、[3,+∞) |
| D、(-∞,-1] |
已知等差数列{an}中,a2=4,a6=12,则公差d等于( )
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
如图所示,AT切⊙O于T,若AT=2
,AE=3,AD=4,DE=2,则BC等于( )

| 6 |

| A、3 | B、4 | C、6 | D、8 |