题目内容
如图,A1B1C1-ABC是三棱柱,下列直线中与AA1成异面直线的是( )


| A、BB1 |
| B、CC1 |
| C、B1C1 |
| D、AB |
考点:空间中直线与直线之间的位置关系
专题:计算题,空间位置关系与距离
分析:根据异面直线的定义,可得结论.
解答:
解:根据异面直线的定义,可得B1C1与AA1成异面直线.
故选:C.
故选:C.
点评:本题考查异面直线的定义,比较基础.

练习册系列答案
相关题目
已知命题“p:x≥4或x≤0”,命题“q:x∈Z”,如果“p且q”与“非q”同时为假命题,则满足条件的x为( )
| A、{x|x≥3或x≤-1,x∉Z} |
| B、{x|-1≤x≤3,x∉Z} |
| C、{-1,0,1,2,3} |
| D、{1,2,3} |
对于非零向量
、
,下列命题中正确的是( )
| a |
| b |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
在区间[0,2]和[1,2]上分别取一个数x,y,则对应的数对(x,y)是不等式x-y≤0的解的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设函数f(x)=
,类比课本推导等差数列前n项和公式的推导方法计算f(-4)+f(-3)+…+f(0)+f(1)+…+f(4)+f(5)的值为( )
| 1 | ||
2x+
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知各项均为正数的数列{an}满足a1=1,an+2an=39(n∈N*),那么数列{an}的前50项和S50的最小值为( )
| A、637 | ||
| B、559 | ||
C、481+25
| ||
D、492+24
|
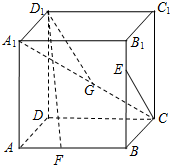 已知正方体ABCD-A1B1C1D1,点E,F,G分别是线段B1B,AB和A1C上的动点,观察直线CE与D1F,CE与D1G.给出下列结论:
已知正方体ABCD-A1B1C1D1,点E,F,G分别是线段B1B,AB和A1C上的动点,观察直线CE与D1F,CE与D1G.给出下列结论: