题目内容
16.已知函数y=2sin(2x+φ)(|φ|<$\frac{π}{2}$)图象经过点(0,$\sqrt{3}$),则该函数图象的一条对称轴方程为( )| A. | x=$\frac{π}{6}$ | B. | x=-$\frac{π}{12}$ | C. | x=$\frac{π}{12}$ | D. | x=-$\frac{π}{6}$ |
分析 由图象过点和题意可得函数解析式,解2x+$\frac{π}{3}$=kπ+$\frac{π}{2}$可得对称轴方程,结合选项可得.
解答 解:∵函数y=2sin(2x+φ)图象经过点(0,$\sqrt{3}$),
∴$\sqrt{3}$=2sinφ,即sinφ=$\frac{\sqrt{3}}{2}$,由|φ|<$\frac{π}{2}$可得φ=$\frac{π}{3}$,
∴y=2sin(2x+$\frac{π}{3}$),令2x+$\frac{π}{3}$=kπ+$\frac{π}{2}$可得x=$\frac{1}{2}$kπ+$\frac{π}{12}$,
∴函数的对称轴方程为x=$\frac{1}{2}$kπ+$\frac{π}{12}$,k∈Z
结合选项可得函数图象的一条对称轴方程为x=$\frac{π}{12}$
故选:C
点评 本题考查正弦函数的对称性,涉及三角函数解析式的求解,属基础题.

练习册系列答案
相关题目
7.如图的框图是一古代数学家的一个算法的程序框图,它输出的结果S表示( )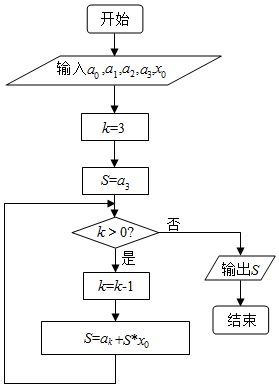

| A. | a0+a1+a2+a3的值 | B. | a3+a2x0+a1x02+a0x03的值 | ||
| C. | a0+a1x0+a2x02+a3x03的值 | D. | 以上都不对 |
4.已知{an}是等差数列,a10=17,其前10项的和S10=80,则其公差d=( )
| A. | 2 | B. | -2 | C. | -1 | D. | 1 |
11.$\frac{{2sin{{47}°}-\sqrt{3}sin{{17}°}}}{{cos{{17}°}}}$=( )
| A. | $-\sqrt{3}$ | B. | -1 | C. | $\sqrt{3}$ | D. | 1 |
1.已知MP、OM、AT分别为θ(0<θ<$\frac{π}{2}$)的正弦弦、余弦线、正切线,若OM<MP<AT,则θ∈( )
| A. | (0,$\frac{π}{4}$) | B. | (0,$\frac{π}{3}$) | C. | ($\frac{π}{4}$,$\frac{π}{2}$) | D. | ($\frac{π}{6}$,$\frac{π}{3}$) |