题目内容
11．$\frac{{2sin{{47}°}-\sqrt{3}sin{{17}°}}}{{cos{{17}°}}}$=（ ）| A． | $-\sqrt{3}$ | B． | -1 | C． | $\sqrt{3}$ | D． | 1 |
分析 由条件利用两角和差的三角公式化简所给的式子，求得结果．
解答 解：$\frac{{2sin{{47}°}-\sqrt{3}sin{{17}°}}}{{cos{{17}°}}}$=$\frac{2sin（30°+17°）-2sin17°•cos30°}{cos17°}$=2•$\frac{sin30°cos17°+cos30°sin17°-cos30sin17°}{cos17°}$
=2sin30°=1，
故选：D．
点评 本题主要考查两角和差的三角公式的应用，属于基础题．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
2．
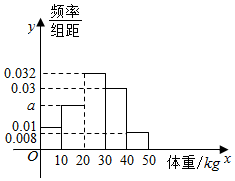如图为教育部门对辖区内某学校的50名儿童的体重（kg）作为样本进行分析而得到的频率分布直方图，则这50名儿童的体重的平均数为（ ）
如图为教育部门对辖区内某学校的50名儿童的体重（kg）作为样本进行分析而得到的频率分布直方图，则这50名儿童的体重的平均数为（ ）| A． | 27.5 | B． | 26.5 | C． | 25.6 | D． | 25.7 |
19．“m=1”是“复数z=m2+mi-1为纯虚数”的（ ）
| A． | 充分但不必要条件 | B． | 必要但不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
6．设i是虚数单位，若复数a-$\frac{17}{4-i}$（a∈R）是纯虚数，则实数a的值为（ ）
| A． | -4 | B． | -1 | C． | 4 | D． | 1 |
16．已知函数y=2sin（2x+φ）（|φ|＜$\frac{π}{2}$）图象经过点（0，$\sqrt{3}$），则该函数图象的一条对称轴方程为（ ）
| A． | x=$\frac{π}{6}$ | B． | x=-$\frac{π}{12}$ | C． | x=$\frac{π}{12}$ | D． | x=-$\frac{π}{6}$ |
3．设函数f（x）=log${\;}_{\frac{1}{2}}$x+x-a，则“a∈（1，3）”是“函数f（x）在（2，8）上存在零点”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
20．已知集合A={x|0＜x＜3}，B={x|x-2＞0}，则集合A∩B=（ ）
| A． | {x|0＜x＜2} | B． | {x|2＜x＜3} | C． | {x|x＞2} | D． | {x|x＞0} |