题目内容
已知α是第四象限角,且f(α)=
(1)若cos(α+
)=
,求f(α)的值;
(2)α=-1860°,求f(α)的值.
| sin(π-α)cos(2π-α) | ||
tan(
|
(1)若cos(α+
| π |
| 2 |
| 1 |
| 5 |
(2)α=-1860°,求f(α)的值.
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:(1)由条件利用诱导公式求得f(α)=sinα,再根据cos(α+
)=
,求得f(α)的值.
(2)由题意可得f(α)=sin(-1860°),利用诱导公式花简求得结果.
| π |
| 2 |
| 1 |
| 5 |
(2)由题意可得f(α)=sin(-1860°),利用诱导公式花简求得结果.
解答:
解:(1)∵已知α是第四象限角,且f(α)=
=
=
=sinα,
∵cos(α+
)=
=-sinα,∴f(α)=sinα=-
.
(2)∵α=-1860°,∴f(α)=sin(-1860°)=sin(-60°-5×360°)=-sin60°=-
.
| sin(π-α)cos(2π-α) | ||
tan(
|
| sinαcosα |
| cotα[-sin(π+α)] |
| sinαcosα | ||
|
∵cos(α+
| π |
| 2 |
| 1 |
| 5 |
| 1 |
| 5 |
(2)∵α=-1860°,∴f(α)=sin(-1860°)=sin(-60°-5×360°)=-sin60°=-
| ||
| 2 |
点评:本题主要考查利用诱导公式进行化简求值,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知M(-3,0),N(3,0),|PM|+|PN|=6,则动点P的轨迹是( )
| A、椭圆 | B、以M,N为端点的线段 |
| C、一条射线 | D、双曲线 |
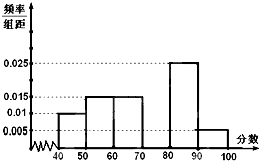 某校从参加高一年级期中考试的学生中抽出60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60)…,[80,90),[90,100],然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高一年级期中考试的学生中抽出60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60)…,[80,90),[90,100],然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题: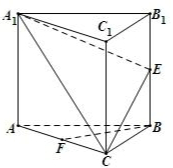 如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.
如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.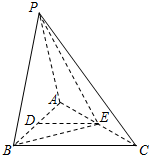 如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点.
如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点.