题目内容
 一半径为2
一半径为2| 2 |
(1)OP旋转的角速度ω是多少(单位:弧度/秒)
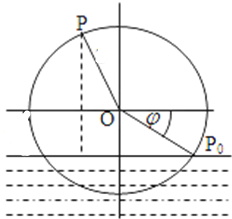
(2)建立如图所示的直角坐标系,设嗲P距离水面的高度z(米)与时间t(秒)的函数关系为z=f(t)=Asin(ωx+φ)+2,其中A>0,而φ(-
| π |
| 2 |
(3)点P第二次到达最高点需要的时间是多少秒?
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:(1)由题意可得,OP旋转的角速度ω=
,计算可得速度ω.
(2)由条件可得f(t)=2
sin(
t+φ)+2,把点(0,0)代入可得sinφ=-
.结合-
<φ<0,可得φ 的值,可得f(t)的解析式.
(3)令 z=f(t)=2
+2,求得t的值.再根据水轮转一周需要
秒,求得点P第二次到达最高点需要的时间.
| 5×2π |
| 60 |
(2)由条件可得f(t)=2
| 2 |
| π |
| 6 |
| ||
| 2 |
| π |
| 2 |
(3)令 z=f(t)=2
| 2 |
| 60 |
| 5 |
解答:
解:(1)由题意可得,OP旋转的角速度ω=
=
(弧度/秒).
(2)易得A=2
,∴z=f(t)=2
sin(
t+φ)+2,
把点(0,0)代入可得sinφ=-
.
结合-
<φ<0,可得φ=-
,∴z=f(t)=2
sin(
t-
)+2.
(3)令 z=f(t)=2
sin(
t-
)+2=2
+2,求得
t-
=
,∴t=4.5(秒).
再根据水轮转一周需要
=12秒,故点P第二次到达最高点需要的时间是4.5+12=16.5秒.
| 5×2π |
| 60 |
| π |
| 6 |
(2)易得A=2
| 2 |
| 2 |
| π |
| 6 |
把点(0,0)代入可得sinφ=-
| ||
| 2 |
结合-
| π |
| 2 |
| π |
| 4 |
| 2 |
| π |
| 6 |
| π |
| 4 |
(3)令 z=f(t)=2
| 2 |
| π |
| 6 |
| π |
| 4 |
| 2 |
| π |
| 6 |
| π |
| 4 |
| π |
| 2 |
再根据水轮转一周需要
| 60 |
| 5 |
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,函数y=Asin(ωx+φ)的图象特征,属于中档题.

练习册系列答案
相关题目
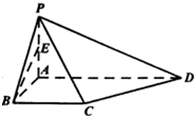 如图,四棱椎P-ABCD的底面为直角梯形,∠ABC=90°,AD∥BC,BA=BC=1,AD=2,PA⊥平面ABCD.
如图,四棱椎P-ABCD的底面为直角梯形,∠ABC=90°,AD∥BC,BA=BC=1,AD=2,PA⊥平面ABCD.