题目内容
已知复数z1=(a+1)+(a-1)i,z2=1+2ai,(a∈R,i是虚数单位).
(1)若复数z1-z2在复平面上对应点落在直线y=x上,求实数a的值;
(2)若复数z1是实系数一元二次方程x2+x+m=0的根,求实数m的值.
(1)若复数z1-z2在复平面上对应点落在直线y=x上,求实数a的值;
(2)若复数z1是实系数一元二次方程x2+x+m=0的根,求实数m的值.
考点:复数的代数表示法及其几何意义
专题:数系的扩充和复数
分析:(1)求出复数z1-z2在复平面上对应点,利用实部等于虚部,求解实数a的值;
(2)利用复数z1是实系数一元二次方程x2+x+m=0的根,它的共轭复数也是方程的根,通过韦达定理求实数m的值.
(2)利用复数z1是实系数一元二次方程x2+x+m=0的根,它的共轭复数也是方程的根,通过韦达定理求实数m的值.
解答:
解:(1)复数z1=(a+1)+(a-1)i,z2=1+2ai,
∴复数z1-z2=a+(-a-1)i,复数z1-z2在复平面上对应点落在直线y=x上,
∴a=-1-1,∴a=-
.
(2)因为虚数z1是实系数一元二次方程x2+x+m=0的根
所以z1+
=-1,即2(a+1)=-1,∴a=-
把a=-
代入,则z1=-
-2i,
所以m=z1•
=
.
∴复数z1-z2=a+(-a-1)i,复数z1-z2在复平面上对应点落在直线y=x上,
∴a=-1-1,∴a=-
| 1 |
| 2 |
(2)因为虚数z1是实系数一元二次方程x2+x+m=0的根
所以z1+
. |
| z1 |
| 3 |
| 2 |
把a=-
| 3 |
| 2 |
代入,则z1=-
| 1 |
| 2 |
所以m=z1•
. |
| z1 |
| 17 |
| 4 |
点评:本题考查复数的代数形式及其几何意义,解题的关键是根据复数的代数形式的几何意义得出参数所满足的不等式,同时考查了运算求解的能力,属于基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
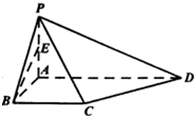 如图,四棱椎P-ABCD的底面为直角梯形,∠ABC=90°,AD∥BC,BA=BC=1,AD=2,PA⊥平面ABCD.
如图,四棱椎P-ABCD的底面为直角梯形,∠ABC=90°,AD∥BC,BA=BC=1,AD=2,PA⊥平面ABCD.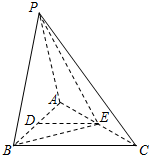 如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点.
如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点.