题目内容
已知函数f(x)=a(x-
)-2lnx(a∈R).
(Ⅰ)若a=2,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)若a>0,求函数f(x)的单调增区间;
(Ⅲ)设函数g(x)=-
.若至少存在一个x0∈[1,e],使得f(x0)>g(x0)成立,求实数a的取值范围.
| 1 |
| x |
(Ⅰ)若a=2,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)若a>0,求函数f(x)的单调增区间;
(Ⅲ)设函数g(x)=-
| a |
| x |
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)将a=2代入,对函数f(x)进行求导得到切线的斜率k=f′(1),切点为(1,f(1)),根据点斜式即可写出切线方程;
(Ⅱ)由题意知先求函数f(x)的定义域,再由(1)得出的导数,设h(x)=ax2-2x+a.下面对a进行分类讨论:①当若0<a<1时,②当a≥1时,由此可知f(x)的单调增区间.
(Ⅲ)存在一个x0∈[1,e]使得f(x0)>g(x0),则ax0>2lnx0,等价于a>
,令F(x)=
,等价于“当x∈[1,e]时,a>F(x)min”.利用导数易求其最小值
(Ⅱ)由题意知先求函数f(x)的定义域,再由(1)得出的导数,设h(x)=ax2-2x+a.下面对a进行分类讨论:①当若0<a<1时,②当a≥1时,由此可知f(x)的单调增区间.
(Ⅲ)存在一个x0∈[1,e]使得f(x0)>g(x0),则ax0>2lnx0,等价于a>
| 2lnx0 |
| x0 |
| 2lnx |
| x |
解答:
解:(Ⅰ)当a=2时,函数f(x)=2(x-
)-2lnx,
f(1)=0,f′(x)=2(1+
)-
.
曲线y=f(x)在点(1,f(1))处的切线的斜率为f′(1)=2.
从而曲线y=f(x)在点(1,f(1))处的切线方程为y-0=2(x-1),
即2x-y-2=0.
(Ⅱ)函数f(x)的定义域为(0,+∞).
∵f′(x)=
,
不妨设h(x)=ax2-2x+a,
当a>0时,△=4-4a2,
①若0<a<1,
由f′(x)>0,即h(x)>0,得
0<x<
或x>
;
∴函数f(x)的单调递增区间为(0,
)和(
,+∞);
②若a≥1,h(x)≥0在(0,+∞)上恒成立,
则f′(x)≥0在(0,+∞)上恒成立,
(Ⅲ)因为存在一个x0∈[1,e]使得f(x0)>g(x0),
则ax0>2lnx0,等价于a>
.
令F(x)=
,等价于“当x∈[1,e]时,a>F(x)min”.
对F(x)求导,得F′(x)=
.
因为当x∈[1,e]时,F′(x)≥0,所以F(x)在[1,e]上单调递增.
所以F(x)min=F(1)=0,因此a>0.时f(x) 在(0,+∞)上单调递增.
| 1 |
| x |
f(1)=0,f′(x)=2(1+
| 1 |
| x2 |
| 2 |
| x |
曲线y=f(x)在点(1,f(1))处的切线的斜率为f′(1)=2.
从而曲线y=f(x)在点(1,f(1))处的切线方程为y-0=2(x-1),
即2x-y-2=0.
(Ⅱ)函数f(x)的定义域为(0,+∞).
∵f′(x)=
| ax2-2ax+a |
| x2 |
不妨设h(x)=ax2-2x+a,
当a>0时,△=4-4a2,
①若0<a<1,
由f′(x)>0,即h(x)>0,得
0<x<
1-
| ||
| a |
1-
| ||
| a |
∴函数f(x)的单调递增区间为(0,
1-
| ||
| a |
1-
| ||
| a |
②若a≥1,h(x)≥0在(0,+∞)上恒成立,
则f′(x)≥0在(0,+∞)上恒成立,
(Ⅲ)因为存在一个x0∈[1,e]使得f(x0)>g(x0),
则ax0>2lnx0,等价于a>
| 2lnx0 |
| x0 |
令F(x)=
| 2lnx |
| x |
对F(x)求导,得F′(x)=
| 2(1-lnx) |
| x2 |
因为当x∈[1,e]时,F′(x)≥0,所以F(x)在[1,e]上单调递增.
所以F(x)min=F(1)=0,因此a>0.时f(x) 在(0,+∞)上单调递增.
点评:本题考查导数的几何意义、导数研究函数单调性及求函数的最值问题,考查学生分析问题解决问题的能力,对于“能成立”问题及“恒成立”问题往往转化为函数最值解决.

练习册系列答案
相关题目
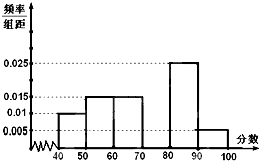 某校从参加高一年级期中考试的学生中抽出60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60)…,[80,90),[90,100],然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高一年级期中考试的学生中抽出60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60)…,[80,90),[90,100],然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题: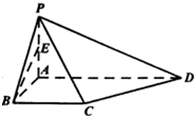 如图,四棱椎P-ABCD的底面为直角梯形,∠ABC=90°,AD∥BC,BA=BC=1,AD=2,PA⊥平面ABCD.
如图,四棱椎P-ABCD的底面为直角梯形,∠ABC=90°,AD∥BC,BA=BC=1,AD=2,PA⊥平面ABCD.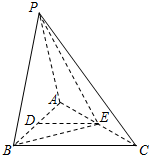 如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点.
如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点.