题目内容

已知二阶矩阵M有特征值λ=3及对应的一个特征向量
e1
=
1
1
，并且矩阵M对应的变换将点（-1，2）变换成（3，0），求矩阵M．
考点：矩阵变换的性质
专题：选作题,矩阵和变换
分析：先设矩阵这里a，b，c，d∈R，由二阶矩阵M有特征值λ=3及对应的一个特征向量
e1
=
1
1
及矩阵M对应的变换将点（-1，2）换成（3，0）．得到关于a，b，c，d的方程组，即可求得矩阵M．
解答： 解：设矩阵M=
ab
cd
，这里a，b，c，d∈R，
则
ab
cd
 
1
1
=3 
1
1
=
3
3
，故
a+b=3
c+d=3
       ①
ab
cd
-1
2
=
3
0
，故
-a+2b=3 
-c+2d=0
        ②
由①②联立解得
a=1
b=2
c=2
d=1
，∴M=
12
21
．
点评：本题主要考查了二阶矩阵，以及特征值与特征向量的计算，属于基础题．
练习册系列答案
相关题目
已知A，B，C三点的坐标分别为A（3，0），B（0，3），C（cosα，sinα），α∈（
π
2
，
3π
2
）．
（Ⅰ）若|
AC
|=|
BC
|，求角α的值；
（Ⅱ）求y=
1
3
（3sinαcosα-
AC
•
BC
+1）的范围．
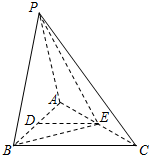如图，在三棱锥P-ABC中，PA=PB=AB=2，BC=3，∠ABC=90°，平面PAB⊥平面ABC，D、E分别为AB、AC中点．
（1）求证：DE∥平面PBC；
（2）求证：AB⊥PE．
数列{an}的前n项和记作Sn，满足 Sn=2an+3n-12（n∈N*）
（Ⅰ）证明数列{an-3}为等比数列，并求出数列{an}的通项公式；
（Ⅱ）记bn=nan，数列{bn}的前n项和为Tn，求Tn．
设数列{an}的前n项和为Sn，已知Sn=2an-2n+1（n∈N*）．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）求证：当x＞0时，ln(x+1)＞
x
x+1
；
（Ⅲ）令cn=(-1)n+1log
an
n+1
2，数列{cn}的前2n项和为T2n．利用（2）的结论证明：当n∈N*且n≥2时，
T
 
2n
＜ln2．
某公司生产A，B，C三款手机，每款均有标准型和豪华型两种型号，某月的产量如表所示（单位：台）．
A B C
标准型 100 150 z
豪华型 300 450 600
按款分层抽样的方法在本月生产的手机中抽取50台，其中A款抽到了10台．
（1）求z；
（2）用分层抽样的方法在C款中抽取一个容量为5的样本，将该样本看成一个总体，从中任取2台，求至少有一台标准型手机的概率；
（3）用随机抽样的方法从B款手机中抽取8台检测性能，经检测它们的评分如下：9.4、8.6、9.2、9.6、8.7、9.3、9.0、8.2．把这8台手机的评分看成一个整体，从中任取一个数，求该数与样本平均数之差的绝对值超过0.5的概率．
将演绎推理：“y=log
1
2
x在（0，+∞）上是减函数”恢复成完全的三段论，其中大前提是
 
．
已知cos（x+
π
6
）=
1
4
，则cos（
5π
6
-x）+cos2（
π
3
-x）的值为
 
．
若复数z满足（3-4i）z=|4+3i|，则z在复平面中所对应的点到原点的距离为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网