题目内容
1．
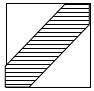如图，在边长为25cm的正方形中挖去边长为18cm的两个等腰直角三角形，现有均匀的粒子散落在正方形中，问粒子落在中间带形区域的概率是多少$\frac{301}{625}$．
分析 粒子落在中间带形区域的概率与阴影部分与正方形的面积比相等，利用几何概型公式得到所求．
解答 解：由题意粒子落在中间带形区域的概率为$\frac{{S}_{阴影部分}}{{S}_{正方形}}$=1-$\frac{18×18}{25×25}$=$\frac{301}{625}$；
故答案为：$\frac{301}{625}$．
点评 本题考查了几何概型的应用；关键是明确粒子落在中间带形区域的概率等于阴影部分与正方形的面积比．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
11．若f（x）和g（x）都是定义在R上的函数，则“f（x）与g（x）同是奇函数或同是偶函数”是“f（x）•g（x）是偶函数”的（ ）
| A． | 充分非必要条件 | B． | 必要非充分条件 | ||
| C． | 充要条件 | D． | 既非充分又非必要条件 |
9．已知sinθ=-$\frac{1}{3}$，且-π＜θ＜-$\frac{π}{2}$，则θ可表示为（ ）
| A． | $arcsin\frac{1}{3}$ | B． | $-\frac{π}{2}-arcsin（-\frac{1}{3}）$ | C． | $-π+arcsin（-\frac{1}{3}）$ | D． | $-π-arcsin（-\frac{1}{3}）$ |
16．若圆C经过坐标原点和点（4，0），且与直线y=1相切，则圆C的方程是（ ）
| A． | ${（x-2）^2}+{（y+\frac{3}{2}）^2}=\frac{25}{4}$ | B． | ${（x-2）^2}+{（y-\frac{3}{2}）^2}=\frac{25}{4}$ | ||
| C． | ${（x+2）^2}+{（y-\frac{3}{2}）^2}=\frac{25}{4}$ | D． | ${（x+2）^2}+{（y+\frac{3}{2}）^2}=\frac{25}{4}$ |
10．方程f（x）=2x+x2-3的零点个数是（ ）
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |